Эффективность алгоритмов

Дата создания: 2009-03-25 12:50:48
Последний раз редактировалось: 2012-02-08 06:29:55

Данная статья - вступительная в разделе "Алгоритмы".

В данном разделе мы сосредоточимся на двух направлениях: структуры данных и непосредственно алгоритмы.

С кое-какими структурами данных Вы уже познакомились: массивы, структуры, классы. Это примеры статических структур данных. Т.е. задали мы вначале программы десять элементов массива, в конце программы этих элементов так и осталось десять. На страницах рассылки и в данном разделе мы познакомимся динамическими структурами данных. Некоторые из этих структур просто делают программистскую жизнь легче, без других невозможно построить определённый алгоритм.

Также структур данных касаются ещё две области программирования, которые мы будем рассматривать: STL и D3DX. В STL (стандартная библиотека шаблонов в C++) собраны математические структуры данных и алгоритмы, а в D3DX (вспомогательная библиотека DirectX) присутствует ряд интересных нам структур, которые непосредственно используются в графических приложениях.

Эффективность алгоритмов

В данном - вступительном выпуске мы не будем рассматривать какую-либо конкретную структуру. Здесь мы поговорим об эффективности алгоритмов. Для этого нам потребуется ввести несколько понятий.

Сразу хочу подчеркнуть, что в данной статье я сознательно упрощаю материал. И с математической точки зрения, некоторые определения в данной статье не корректны. За более точным и полным описанием математических понятий, вам потребуется обратиться к учебникам по алгоритмам.

Приступим. Есть несколько критериев оценки эффективности алгоритмов. Для простоты мы будем обсуждать только временную эффективность.

Казалось бы временная эффективность должна выражаться в секундах. Но в данном случае это не так. потому что один и тот же алгоритм на разных компьютерах выполнится за разное количество времени.

Рассмотрим пример: у нас есть массив из десяти элементов. И у нас есть два алгоритма: поиск элемента в массиве и сортировка массива.

Первый алгоритм ищет в массиве определённое значение. Например, нужно проверить есть ли в массиве число 14. Для этого каждый элемент массива сравнивается с этим числом.

Второй алгоритм выстраивает элементы массива по возрастанию. Для этого ищется самое маленькое значение и помещается в начало, затем ищется следующее значение и так далее, пока в начале массива не окажется самый маленький элемент, а в конце - самый большой.

Что у нас здесь есть? Прежде всего размер входных данных. Обозначим его - n. Из нашего примера n = 10.

Так вот, эффективность алгоритма - это функция зависящая от размера входных данных. Чем больше входных данных, тем дольше будет выполняться алгоритм.

Функция в математическом контексте и в программистском понимается примерно одинаково. Есть различия, но пока они для нас несущественны.

При выполнении алгоритма для каждого входного значения выполняется какая-то базовая операция. В алгоритме поиска - это простое сравнение. При сортировке базовая операция посложнее. Базовая операция тоже влияет на эффективность алгоритма.

В данном примере эффективность алгоритма удобно понимать не как функцию, а как цикл. Смотрите: у нас есть набор входных данных в количестве n. n - это количество повторений цикла. А базовая операция - это тело цикла.

Порядок роста

Теперь нам нужно рассмотреть зависимость изменения количества базовых операций необходимых для выполнения алгоритма от увеличения размера входных данных.

Пример: у нас есть упорядоченный массив из 10 элементов. Представим, что нам нужно найти два числа. Во время поиска оказалось, что первое число находилось в середине массива, а второе - в конце. Теперь возьмём массив из 20 элементов (в два раза больше). И опять, элементы расположены так, что первый элемент оказался в середине, а второй в конце. Эти два случая имеют одинаковый порядок роста: при увеличении размера входных данных в два раза, количество базовых операций необходимых для выполнения алгоритма увеличилось в два раза.

Примечание: заметьте, что хотя мы и используем один алгоритм в примере, но рассматриваем два случая выполнения этого алгоритма. В данном контексте мы можем говорить о двух разных алгоритмах. Это важно!

Теперь переходим к самому важному в статье.

Сравнение порядков роста

Количество базовых операций за которое выполняется алгоритм - это время выполнения алгоритма. Обозначим его как t(n).

И обозначим какую-нибудь простая функция g(n) с которой мы будем сравнивать время выполнения t(n).

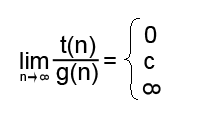
Для сравнения порядков роста двух алгоритмов используют предел отношения времени выполнения двух алгоритмов.

При постоянно увеличивающемся n мы вычисляем отношение t(n) к g(n).

В первом случае t(n) имеет меньший порядок роста. При увеличении размера входных данных, знаменатель будет расти намного быстрее числителя. Соответственно чем больше n, тем результат будет ближе к нулю.

Во втором случае порядок роста t(n) и g(n) одинаковый. с - какая-то константа. Т.е. при увеличении размера входных данных, насколько вырос порядок роста t(n) настолько же вырос и порядок роста g(n).

В третьем случае t(n) имеет больший порядок роста. Соответственно результат стремится к бесконечности.

Ну, вот в общем то и всё. Тема на первый взгляд не сильно нужная, но иногда бывает очень нужно выразить эффективность алгоритма числом. Практическое применение материала из данной статьи Вы увидите в последующих уроках этого раздела.