Выбор объектов в трёхмерном пространстве (Object picking)

Дата создания: 2010-03-04 11:39:03
Последний раз редактировалось: 2012-03-01 02:13:16

Cегодня мы будем учиться выбирать объекты в трёхмерном пространстве.

В прошлом уроке мы научились взаимодействовать с двухмерными объектами. Но в огромном количестве игр требуется взаимодействие не только с элементами интерфейса, но и трёхмерными объектами. Например, выбор юнитов в стратегиях.

Существует много способов взаимодействия с трёхмерными объектами. Мы рассмотрим самый простой (проще нет в природе), но редко встречающийся.

Итак, приступим.

Координаты курсора мыши

Прежде всего, нужно получить координаты курсора мыши.

Напоминаю, что мы знаем два способа: DirectInput (метод GetDeviceState), WinAPI (поля сообщения WM_MOUSEMOVE). Первый способ использовался в программе "Камера", второй в программе "Клетки". Давайте посмотрим на разницу между ними.

В полях сообщения WM_MOUSESTATE хранятся координаты курсора мышки относительно левого верхнего угла окна. Т.е. начало координат окна расположено в левом верхнем углу. Ось x идёт слева направо. Ось y идёт сверху вниз. В случае использования IDirectInputDevice8::GetDeviceState в полях структурной переменной DIMOUSESTATE будут сохранены новые координаты курсора мыши относительно текущей позиции.

Для наглядности давайте посмотрим на картинку:

Слева показана позиция курсора относительно левого верхнего угла окна. Справа показана позиция курсора относительно самого себя. Во втором случае пользователь передвинул курсор на 25 единиц вправо. Используя одно из представлений координат, можно без проблем перейти в другое. Просто для разных ситуаций наилучшим образом подходит только одно представление координат.

В сегодняшнем примере мы будем использовать координаты относительно левого верхнего угла окна. В упражнении вам необходимо будет воспользоваться представлением координат относительно текущей позиции курсора. Теперь взглянем на заготовку кода:

float x=0,y=0;

// начало основного цикла

if (msg.message == WM_MOUSEMOVE)
{
  x = LOWORD(msg.lParam);
  y = HIWORD(msg.lParam);
}

Почти такой же код мы использовали в прошлом уроке. В данном отрывке мы получаем координаты курсора мыши относительно левого верхнего угла окна. Обратите внимание на тип переменных x и y.

Выбор объектов

Ну а теперь у нас начинаются сложности. Что делать с координатами курсора? Когда речь идёт о двухмерной графике, то там всё просто: любой элемент интерфейса или спрайт находится в одном координатном пространстве с курсором мыши - в координатном пространстве (двухмерной плоскости) окна. Но трёхмерные объекты создаются относительно абсолютного центра (начала мировых координат). Как связать трёхмерное пространство, в котором определены игровые объекты и двухмерное, в котором определены элементы интерфейса и, что самое важное, курсор мышки. Обычно для решения этой задачи используются преобразования. Но тут всё довольно сложно. Мы же пойдём по гораздо более простому пути. Теме более у нас уже всё для этого готово.

Для сегодняшнего примера я использовал программу "Камера" и разработанные для неё классы и функции. Размер окна стандартный - 500 на 500. Также я убрал заголовок окна (использовал стиль WS_POPUP).

Давайте взглянем на рисунок, который даст более наглядное представление нашей задаче:

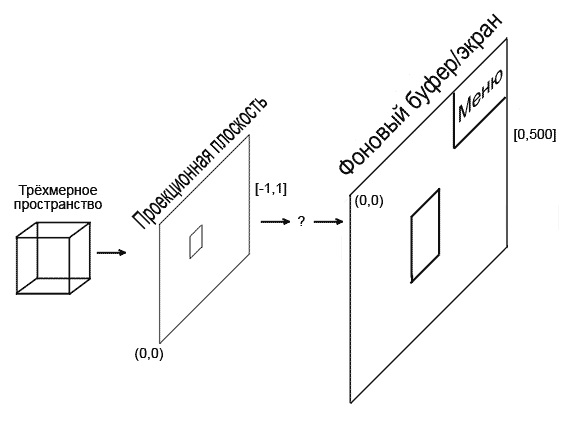
Что мы здесь видим:

- Объекты в проекционной плоскости находятся в диапазоне [-1; 1] (это получается в результате перемножения точек на проекционную матрицу). Если после всех преобразований и деления на четвёртую компоненту, точка будет находиться внутри отрезка от -1 до 1 включительно, то эта точка будет выведена на экран.

- Объекты в фоновом буфере находится в диапазоне [0; 499] (на картинке ошибка, должно быть не 500, а 499; извините, лень было исправлять).

- Оси y в проекционной плоскости и в итоговом изображении направлены в разные стороны.

Давайте ещё раз вспомним, как мы создавали трёхмерное изображение: преобразование из объектного пространства в мировое, затем в пространство камеры, затем в проекционную плоскость. После этого, получившееся значение мы делили на четвёртую компоненту. Выполнив все эти действия над вершинами, мы получили картинку в проекционной плоскости на рисунке выше.

Но смотрите, после этого преобразования над точками не заканчиваются (2-ой и 3-ий пункт). В DirectX невозможно получить доступ к этим этапам преобразований. Эти этапы DirectX выполнит самостоятельно: проецирование с проекционной плоскости (размер 2 на 2) в фоновый буфер (размер окна) и смена направления оси y. Вообще говоря, с помощью проекционной матрицы можно сразу спроецировать на плоскость любого размера. Но мы вынуждены играть по правилам DirectX, а эта библиотека требует проекционную плоскость 2 на 2. Проецированием на плоскость окна DirectX занимается самостоятельно.

Наша задача: сделать обратное преобразование точки на экране (позиция курсора) в проекционную плоскость. Поменять направление оси y очень просто: нужно домножить ординату (значение y) точки на минус единицу.

Теперь осталось спроецировать координаты с отрезка [0; 499] в отрезок [-1; 1]. Рассмотрим только значение x (для y всё то же самое, плюс умножение на -1).

Сначала рассмотрим проецирование на экран. Для наглядности вот рисунок:

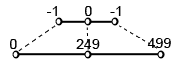
Если немного подумать, то становится очевидным, что сначала нужно домножить абсциссу и ординату на половину ширины и высоты окна. А затем к получившемуся значению прибавить половину ширины и высоты.

Нам же нужна обратная проекция. Поэтому сначала мы будем отнимать половину ширины или высоты окна, а затем делить на половину ширины/высоты.

Посмотрим на код преобразования позиции курсора в проекционную плоскость:

lmb = 0;
x = 0; y = 0;
if (msg.message == WM_MOUSEMOVE)
{
  x = LOWORD(msg.lParam);
  y = HIWORD(msg.lParam);
  x = (x - 250) / 250;
  y = (y - 250) / 250 * -1;
}

Хорошо разберитесь как происходит преобразование из проекционной плоскости в плоскость экрана и наоборот. Вам поможет вышеприведённый рисунок. Также можете взять несколько точек и посчитать преобразования на листке бумаги.

Ура! Мы только что закончили рассмотрение всех этапов преобразования: от создания точки в локальном пространстве, до вывода её на экран. Теперь вы можете сымитировать трёхмерное пространство на любом языке программирования, где есть возможность вывода прямых линий (можно обойтись только точками). Конечно, у нас ещё осталось одно белое пятно: создание матрицы камеры. Но не будем омрачать радостный момент...

Теперь вернёмся к выбору объектов. С этого момента и до конца урока мы будем работать только в проекционном пространстве.

В данный момент все треугольники и позиция курсора мышки находятся в одном координатном пространстве. Самое важное для нас (это сильное упрощает задачу), что все объекты теперь расположены в двухмерном пространстве (это не совсем так, но координату z можно просто отбросить).

Для каждого трёхмерного объекта мы будем проверять, находится ли курсор мыши внутри одного из треугольников объекта. Для простоты будем рассматривать модель, состоящую из одного треугольника.

Тут нас поджидает очередная трудность. Как в двухмерном пространстве проверить, находится ли точка внутри треугольника? Для этого нужно знать, что такое барицентрические координаты. Ндаа... Мы пока что ещё и не слышали о таких вещах. Поэтому придётся хитрить.

Мы воспользуемся наиболее понятным (на мой взгляд) способом определения вхождения точки в треугольник. При этом нам придётся мириться с довольно большой погрешностью.

А делать мы будем следующее: Каждый треугольник мы будем достраивать до прямоугольника со сторонами параллельными координатным осям (сторонам экрана). Посмотрим на картинку:

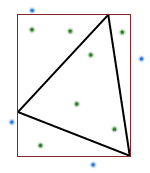
Чёрным цветом показан прямоугольник, столкновение с которым нужно проверять. Красным цветом показан прямоугольник, столкновение с которым будет проверяться. Зелёным цветом показаны точки, для которых будет считаться, что они находятся внутри треугольника. Голубым цветом показаны точки, для которых будет считаться, что они находятся за пределами треугольника.

Посмотрим на код. Для примера я использовал программу "Камера", предварительно убрав весь код связанный с перемещением объектов:

float left=0,top=0,right=0,bottom=0;
bool frustumPicked = 0;
for (int i = 0; i < 12; i++)
{
  x1 = frustum[frustumIndexes[i*3]].x;
  y1 = frustum[frustumIndexes[i*3]].y;
  x2 = frustum[frustumIndexes[i*3+1]].x;
  y2 = frustum[frustumIndexes[i*3+1]].y;
  x3 = frustum[frustumIndexes[i*3+2]].x;
  y3 = frustum[frustumIndexes[i*3+2]].y;

  left = minimum(x1,x2,x3);
  top = maximum(y1,y2,y3);
  right = maximum(x1,x2,x3);
  bottom = minimum(y1,y2,y3);

  if (x > left && x < right &&
    y < top && y > bottom)
  {
    frustumPicked = 1;
    // сброс флагов выбора других объектов
    break;
  }
}

Здесь показан код проверки выбора пирамиды (frustum). Обратите внимание, что здесь не используется структура RECT. Её вполне можно было бы использовать, если бы её поля могли хранить не только целые числа (long).

Флаг frustumPicked (pick - выбирать) служит для проверки, выбрана пирамида или нет. Для других объектов также должны существовать подобные переменные.

В цикле 12 итераций - по количеству треугольников в модели.

Вначале происходит вытаскивание координат трёх вершин треугольника. Для этого используется массив преобразованных вершин (frustum) и массив индексов (frustumIndexes). Более подробно значения этих массивов описывались в уроке по созданию камеры.

После этого происходит "построение" прямоугольника. Для этого нужно найти максимальные и минимальные значения x и y трёх точек.

Функции minimum и maximum очень простые. В них находится максимальное или минимальное значение трёх чисел. Приведу код только функции minimum:

float minimum (float a, float b, float c)
{
  if (a < b)
    if (a < c)
      return a;
  if (b < a)
    if (b < c)
      return b;
  if (c < a)
    if (c < b)
      return c;
}

После этого происходит уже хорошо знакомый нам тест столкновения точки (позиция курсора) и прямоугольника. Обратите внимание, как только установлено, что курсор мыши был наведён на один из треугольников, происходит выход из цикла (оператор break).

Вот собственно и всё. Теперь осталось выполнить какое-нибудь действие с объектом. В своём примере я просто менял цвет модели:

if (frustumPicked == 0)         // пирамида не выбрана
  for (int i = 0; i < 8; ++i)
    frustum[i].color = 0xff555555;
else if (frustumPicked == 1)    // пирамида выбрана
  for (int i = 0; i < 8; ++i)
    frustum[i].color = 0xff000000;

Заключение

Как я уже писал выше, это почти что самый простой способ выбора объектов в трёхмерном пространстве. Но он не используется в современных программах.

Дело в том, что обычно нет доступа к значениям вершин преобразованных в проекционную плоскость (у нас-то он есть, поэтому мы и смогли им воспользоваться). В данном случае позицию курсора представляют в виде луча, который преобразуют в мировое или даже локальное координатное пространство. Далее возможны два основных варианта: столкновение с треугольниками (проверяются барицентрические координаты) или столкновение луча с AABB. Оба метода мы ещё будем рассматривать более подробно. Кстати, построение AABB очень сильно напоминает то, что мы делали сегодня (построение прямоугольника вокруг треугольника). Но всему своё время.

Также хотелось бы упомянуть, что проверка всех треугольников модели не самый оптимальный способ.

Теперь по поводу точности попадания по модели с помощью метода описанного выше. На первый взгляд, кажется, что погрешность слишком большая. На последней картинке "активное" пространство (где будет засчитано попадание по треугольнику) почти в два раза больше площади самого треугольника. Но на самом деле погрешность не такая уж и большая. Через несколько урокво, когда мы начнём загружать модели в наши программы, мы убедимся, что погрешность будет вообще не заметна, так как треугольники будут очень маленькими.

В предыдущем абзаце я упомянул о загрузке моделей в наши программы. До этого замечательного дня осталось 3-4 урока. Т.е. мы уже совсем близко подошли к созданию настоящих игр! Но до этого нам нужно сделать несколько важных вещей. Прежде всего - включить освещение.

Упражнения

1. Создайте программу, в которой можно выбирать трёхмерные объекты. Если за основы вы возьмёте программу "Камера", то обязательно поменяйте ориентацию всех объектов, хотя бы на один градус в любом направлении.

2. Создайте программу из пункта 1, используя для ввода DirectInput. Значения координат относительно текущего положения курсора вам нужно будет самостоятельно преобразовывать в координаты относительно левого верхнего угла окна.

3. В программе из пункта 2 используйте уровень взаимодействия с операционной системой: DISCL_FOREGROUND | DISCL_EXCLUSIVE . При этом вам понадобится нарисовать курсор в любом графическом редакторе (например, в paint). А в программе рисовать его самостоятельно. Обратите внимание, paint не умеет сохранять bmp в 32-битном формате.

4. Для программы из пункта 1 выведите на экран прямоугольник, с которым было столкновение курсора мыши. В своей программе я сделал рамку красным цветом толщиной в два пикселя. Картинка для наглядности (зелёным цветом я показал, куда тыкал мышкой):

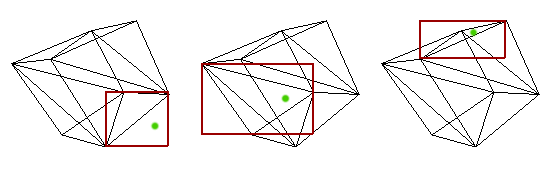
На сегодня всё. До скорой встречи.