Растеризация треугольников (triangle rasterization)
Дата создания: 2010-04-14 20:29:52
Последний раз редактировалось: 2012-10-31 20:03:54
Сегодня будем разбирать программу клетки v0.3. Первоначально у неё было гораздо больше возможностей. Но чтобы сократить урок, я серьёзно порезал код.
Урок разделён на три основные части: в первой части разбираются нерассмотренные моменты из предыдущих уроков, во второй рассмотрен новый интерфейс, а третья часть посвящена растеризации прямых линий и треугольников.
Прежде чем начнёте читать урок, разберитесь с уравнением прямой (один из предыдущих уроков).
Исходный код и сборку можно скачать из раздела "листинги и программы". Все картинки для интерфейса лежат в архиве с исполняемым файлом. Перед запуском программы обязательно добавьте в папку с проектом папку images из сборки.
О разном
Прежде чем мы приступим, давайте рассмотрим несколько вещей, которые не были освещены в предыдущих уроках, но будут использоваться в программе клетки v0.3.
Когда мы загружали информацию из файла (в частности, bmp-файлы), мы считывали её последовательно, байт за байтом.
В потоках есть указатели чтения и записи, которые позволяют "перемещаться" по потоку в поисках нужной информации. Для перемещения в потоках используются два метода: seekg позиционирует указатель чтения, tellg позиционируют указатель записи. Перегружено два варианта этих методов: с одним аргументом и с двумя.
При вызове одной из этих функций с одним аргументом, в функцию передаётся смещение в байтах от начала файла. Примеры:
is.seekg(10); // чтение начнётся с 10-ого байта os.tellg(0); // запись начнётся с начала файла
Вариант с двумя аргументами позволяет указать, относительно чего будет осуществляться сдвиг: относительно начала файла (beg, beginning - начало), относительно текущей позиции (cur, current - текущий), относительно конца файла (end, end - конец).
Статичные константы cur, beg, end принадлежат классу ios, поэтому используются вот так: ios::cur, ios::beg, ios::end. Если вы не используете стандартное пространство имён (через using namespace std), то перед ios нужно указать пространство имён. Вот как будут выглядеть вызовы методов seekg и tellg с двумя аргументами:
is.seekg(-10, std::ios::end); // 10 байт "влево" от конца файла os.tellg(15, std::ios::cur); // 15 байт "вправо" от текущей позиции using namespace std; is.seekg(5, ios::cur); // теперь указатель чтения в пяти байтах от конца файла.
С этим разобрались. Теперь вспомним уравнение прямой:
y = kx + b
Чтобы построить прямую, нужно знать её направление и одну точку. В математике довольно строго определяется и направление (dy/dx), и точка (берётся точка пересечения прямой с осью y). На практике коэффициент k можно представить и как dx/dy - ничего не изменится (новый коэффициент - 1/k). Кроме того не всегда известна точка b, но почти всегда известны координаты двух точек или уравнение прямой и координаты одной точки.
Допустим, у нас на экране монитора есть точка, через которую будет проходить прямая. Точка задана координатами (x1,y1). Подставим координаты первой точки в уравнение:
y1 = k*x1 + b
Чтобы избавиться от b необходимо из уравнения прямой вычесть то, что получилось у нас:
y = k*x + b - y1 = k*x1 + b =-------------- (y-y1) = k*(x-x1)
Это уравнение прямой проходящей через данную точку плоскости с координатами (x1,y1). В данном уравнении нам удалось избавиться от b. Ещё раз повторю, значения x1,y1 известны. Пусть x1 = 2, y1 = 3. Тогда:
(y-3) = k*(x-2)
Подставляя вместо x и y координаты произвольной точки, можно определить, принадлежит ли эта точка данной прямой или нет.
Теперь, когда мы выяснили, что вместо b в уравнении можно использовать произвольную точку, принадлежащую этой прямой, давайте разберёмся с коэффициентом k.
k позволяет определить направление прямой. Этот коэффициент задаётся как dy/dx. Необходимо хорошо понимать смысл этого отношения. Пусть нам известна вторая точка лежащая на прямой: x2 = 3, y2 = 5. Посчитаем dx и dx:
dx = x2 - x1 = 3 - 2 = 1 dy = y1 - y1 = 5 - 3 = 2 k = dy/dx = 2/1 = 2
Какой смысл у этой двойки? Когда x увеличивается на единицу, y увеличивается на 2. Т.е. y растёт быстрее. Теперь зададим другую прямую, проходящую через ту же точку. x2 = 4, y2 = 4:
dx = 4 - 2 = 2 dy = 4 - 3 = 1 k = dy/dx = 2/1 = 0,5
В данном случае, когда значение y увеличивается на 1, значение x увеличивается на 2. 0,5 означает, что y растёт в два раза медленнее чем x.
Рассмотрим направление прямой (от нуля до 90 градусов) в зависимости от значения k:
1. k = 0, когда dy = 0. При этом прямая параллельна оси x.
2. k > 0 && k < 1, когда dx > dy. Т.е. в этом случае значение x растёт быстрее y - прямая "пологая".
3. k = 1, когда dx == dy. В этом случае значения x и y растут с одинаковой скоростью - угол прямой 45 градусов.
4. k > 1 (до бесконечности), когда dy > dx. В этом случае значение y растёт быстрее x - прямая "крутая".
5. Отдельно - dx=0. В этом случае коэффициент не определён. Прямая параллельна оси y.
При смене знака k, прямая симметрично отображается относительно оси y. На рисунке ниже показаны все возможные значения k при разном направлении прямой:
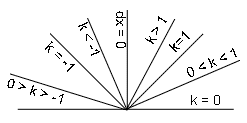
При программировании нужно учесть все эти случаи.
Создание интерфейса компьютерной игры
Если в программе клетки v0.2 вы руководствовались примерами из 25-ого выпуска, то проверку всех элементов интерфейса вы сделали в основном цикле. При этом тело цикла превращается в нечто нечитаемое. Решению этой проблемы будет посвящена первая часть выпуска.
Мы создадим класс для элементов интерфейса, который можно очень легко использовать в самых различных ситуациях. Интерфейс будет основан на прямоугольных кнопках. Пока что мы ещё не можем написать сложные элементы: полосы прокрутки, ползунки, стыкующиеся окна, вкладки.
Нам нужно так организовать данные, чтобы было очень легко добавлять новые элементы интерфейса и обрабатывать нажатия мышки на них.
Сначала напишем класс, в котором хранится отдельный элемент:
class IntObject
{
public:
bool active;
bool visible;
int parent;
int x,y;
int width, height;
int* img;
IntObject(char* fname)
{
active = 0;
visible = 0;
parent = 0;
x = 0; y = 0;
img = NULL;
std::ifstream is (fname,std::ios::binary);
is.seekg(18);
is.read(reinterpret_cast(&width),sizeof(width));
is.read(reinterpret_cast(&height),sizeof(height));
is.seekg(28,std::ios::cur);
img = new int[width*height*32/8];
for (int i = height - 1; i >= 0; --i)
is.read(reinterpret_cast(img)+i*width*32/8,width*32/8);
is.close();
}
~IntObject()
{
if (img != NULL)
delete [] img;
img = NULL;
}
void DrawIntObject(D3DLOCKED_RECT& lockedRect)
{
for (int i = 0; i < height; ++i)
for (int j = 0; j < width; ++j)
if (img[j+i*width] != 0x00ffffff)
memcpy(reinterpret_cast(lockedRect.pBits)
+y*lockedRect.Pitch // смещение от верхнего края окна
+x*4 // смещение от левого края окна
+i*lockedRect.Pitch // смещение от верхней границы элемента
+j*4, // смещение от левой границы элемента
reinterpret_cast(&img[j+i*width]),4);
}
};
Класс довольно простой. Я его назвал IntObject (от Interface Object). Все данные объявлены как public.
active:
Данное поле позволяет сказать, активен ли элемент, т.е. произойдёт ли какое-нибудь событие, если на него щёлкнуть.
visible:
Данное поле позволяет сказать, видим ли элемент в данный момент (visible - видимый). 1 - элемент видим (рисуется), 0 - элемент невидим (не рисуется).
parent:
Родительский элемент. Это поле позволяет группировать элементы интерфейса. Например, в меню доступно два пункта. У этих пунктов родительским элементом является меню.
x,y:
Координаты элемента относительно левого верхнего угла окна.
width, height:
Ширина и высота элемента интерфейса. Заметьте, в данном случае размеры и координаты интерфейса мы задали через x,y,width,height. Это можно было бы сделать и по-другому: left,right,width,height - используется в структуре RECT; x1,y1,x2,y2 - в этом случае ширину и высоту пришлось бы считать в ручную, с другой стороны здесь сразу доступны координаты всех четырёх углов.
img:
Указатель на int. Это поле используется для хранения картинки (скина) текущего элемента.
В определении класса перегружен конструктор для одного аргумента. Аргумент - имя файла картинки создаваемого элемента. В конструкторе все поля обнуляются, затем создаётся поток и открывается файл. Обратите внимание, что в данном случае мы не считываем весь заголовок, а с помощью функции seekg переходим сразу к ширине и высоте картинки, которые считываются в поля width и height. После этого указатель чтения файла перемещается непосредственно к началу картинки.
Перед тем как начнётся считывание картинки, для неё выделяется память. В скобках используется вот такое выражение: width*height*32/8. Если вы не знаете, в каком формате хранятся пиксели, создаваемых вами картинок (не во всех редакторах можно выбирать формат), или если вы будете смешивать мои картинки со своими, то вам понадобится считать информацию о количестве байт на пиксель из заголовка. А при выделении памяти вместо 32 подставить соответствующую переменную. Так как у меня все картинки в 32-битном формате, я использовал константу.
В цикле происходит декрементирование счётчика, так как в bmp картинки хранятся в перевёрнутом виде. Информация считывается построчно. Если в ваших файлах на пиксели отводится меньше 32 бит, то вам нужно вручную добавлять недостающие байты, чтобы формат пикселей картинки соответствовал формату пикселей фонового буфера.
В деструкторе происходит освобождение памяти.
Единственный метод класса рисует (draw - рисовать) изображение. Аргумент - указатель на D3DLOCKED_RECT. Это говорит нам о том, что когда вызывается метод DrawIntObject, фоновый буфер уже замкнут. В прошлых программах мы замыкали буфер для каждого графического элемента. В этой программе буфер замыкается только один раз. При этом замыкается вся поверхность (всё окно). Именно поэтому, в классе IntObject есть переменные x,y - теперь не нужно для каждого элемента хранить структурную переменную RECT.
В методе всё стандартно: изображение выводится попиксельно слева направо, сверху вниз. При этом белые пиксели не копируются.
Важно: нельзя вызывать конструктор без аргументов, так как в таком случае не будет загружено изображение. Конструктор без аргументов можно поместить в private, тогда при попытке вызова этого конструктора, выскочит ошибка. Также нужно обязательно правильно указывать имя файла при вызове конструктора с одним аргументом. Вот и всё что есть в классе IntObject. Теперь обратим внимание на то, чего нет в этом классе. В нём нет никакой информации о действиях объектов.
Здесь мы столкнулись с очень интересным видом классом: все его экземпляры должны выполнять разные задачи. Как у нас было раньше? Например, в программе камера: объекты класса MovObject могли перемещаться и менять ориентацию в пространстве. Или, другой пример, юниты в игре: они все могут выполнять одинаковые задачи (методы класса). Все объекты класса IntObject выполняют разные задачи. Т.е. один экземпляр закрывает программу, другой рисует сетку, третий открывает меню... Пример:
bool gridFlag = 0; // сетка
IntObject grid("путь к картинке");
// задание полей grid
Как в таком случае заставить объект grid менять значение переменной gridFlag? Существует несколько решений. Сейчас мы познакомимся с одним из них. Главное здесь то, что в классе IntObject нет информации о том, как должен вести себя отдельный объект.
Таблица элементов интерфейса
Все элементы интерфейса будут храниться в одномерном массиве указателей на IntObject. Использование указателей позволяет легко добавлять новые, удалять старые элементы. Кроме того, в будущем мы получим ещё массу бонусов от использования именно указателей, а не просто объектов.
Массив, содержащий указатели на все элементы интерфейса, мы будем называть таблицей объектов/элементов интерфейса - это обычный массив. Таблица элементов определяется в глобальной области видимости:
const int NUM_INT_ELEMENTS = 25; IntObject* intTable[NUM_INT_ELEMENTS];
NUM_INT_ELEMENTS - количество элементов в таблице. Так как нам нужно как-то различать отдельные элементы (ведь у каждого своя задача), определим ряд констант:
const int SKIN = 0; // основная подложка const int MENU = 1; // подложка меню const int GRID = 2; // кнопка сетки const int MENU_BUTTON = 3; // кнопка "Меню" const int EXIT = 4; // кнопка "Выход" в меню const int RETURN = 5; // кнопка "Вернуться" в меню const int ERASE = 6; // кнопка очистки поля const int TRIANGLE_POINTS = 7; // кнопка для вывода треугольников точками const int TRIANGLE_EDGES = 8; // кнопка для вывода треугольников гранями const int TRIANGLE_FILLED = 9; // кнопка для вывода закрашенных треугольников
Можно было бы эти константы определить в перечислении, но я уже не стал переделывать. Константы используются для доступа к элементам таблицы объектов - каждая константа отвечает за свой элемент в таблице интерфейса. Здесь задано 10 констант (десять элементов интерфейса), а количество объектов в таблице - 25. Ничего страшного в этом нет. Остальные объекты могут быть не определены: с 10-ого по 24-й. Или же вы можете изменить NUM_INT_ELEMENTS.
Теперь нужно заполнить таблицу интерфейса. Это происходит в функции InitGraphics. Всю функцию я приводить не буду, она слишком большая. Лишь часть:
intTable[SKIN] = new IntObject("images/interface.bmp");
intTable[MENU] = new IntObject("images/menu.bmp");
intTable[GRID] = new IntObject("images/grid.bmp");
intTable[EXIT] = new IntObject("images/exit.bmp");
intTable[SKIN]->x = 0;
intTable[SKIN]->y = 0;
intTable[SKIN]->active = 0;
intTable[SKIN]->visible = 1;
intTable[SKIN]->parent = 0;
intTable[MENU]->x = 151;
intTable[MENU]->y = 76;
intTable[MENU]->active = 0;
intTable[MENU]->visible = 0;
intTable[MENU]->parent = 0;
intTable[EXIT]->x = 192;
intTable[EXIT]->y = 113+36*3;
intTable[EXIT]->active = 0;
intTable[EXIT]->visible = 0;
intTable[EXIT]->parent = MENU;
Вначале создаются элементы. Для доступа к индексам мы используем определённые константы. Затем заполняются поля экземпляров IntObject. Поля width и height к этому моменту уже заданы - при вызове конструктора. Остановимся на поле parent. У двух элементов это поле равно нулю: SKIN и MENU. SKIN - основной фон программы (смотрите файл interface.bmp), MENU - фон меню (файл menu.bmp). У всех остальных элементов родительским (parent) является или MENU, или SKIN. Так как при запуске программы меню закрыто, то оба элемента, у которых parent=MENU, невидимы и неактивны (это элементы RETURN и EXIT).
Это, наверное, самая сложная часть в новом интерфейсе: его долго заполнять.
Теперь взглянем на начало основного цикла, так как в программе я использовал новый для нас способ определения координат мыши:
while (1)
{
lmb = 0;
if (PeekMessage(&msg, NULL, 0, 0, PM_REMOVE))
{
if (msg.message == WM_QUIT)
break;
TranslateMessage(&msg);
DispatchMessage(&msg);
if (msg.message == WM_LBUTTONUP)
{
lmb = 1;
x = msg.pt.x-200;
y = msg.pt.y-100;
}
}
// остальной код
В данном случая для определения нажатия левой клавиши мышки используется сообщение WM_LBUTTONUP (up - вверх). Это сообщение посылается системой, когда пользователь отпускает левую кнопку мыши. Напоминаю, что в прошлой версии мы использовали сообщение WM_LBUTTONDOWN (down - вниз) - это сообщение посылается, когда была нажата кнопка мышки. Помимо этого в версии 0.3 не проверяется сообщение WM_MOUSEMOVE, которое мы использовали для того, чтобы вытащить координаты курсора. Координаты курсора мы получим другим способом:
Структуры MSG и POINT
Давайте взглянем на структуру MSG, с помощью которой в WinAPI передаются сообщения:
typedef struct {
HWND hwnd;
UINT message;
WPARAM wParam;
LPARAM lParam;
DWORD time;
POINT pt;
} MSG, *PMSG;
Первые четыре параметра нам хорошо знакомы. time - это момент времени, когда было создано сообщение. И последний параметр - переменная типа POINT. Это тоже структура. Её определение:
typedef struct tagPOINT {
LONG x;
LONG y;
} POINT, *PPOINT;
Назначение этой структуры, думаю, объяснять не нужно. Так вот, оказывается, в поле pt структуры MSG передаются координаты курсора. Единственная проблема - координаты даны относительно экрана, а не окна. Чтобы преобразовать эти координаты к координатам окна, нужно из x и y вычесть отступы от начала экрана. Это четвёртый и пятый аргументы функции CreateWindow. Именно это и происходит в начале основного цикла.
Теперь, если была отпущена левая кнопка мыши lmb = 1, а в переменных x и y хранятся координаты курсора мышки в момент, когда пользователь отпустил левую кнопку.
Далее в основном цикле проверяются все элементы интерфейса с помощью всего одного вызова функции:
if (lmb == 1) CheckInt(x,y);
Функция CheckInt (check - проверить) принимает координаты курсора и проверяет, был ли выбран какой-нибудь из активных элементов интерфейса. Напоминаю, что эта функция вызывается только в случае, когда была нажата левая клавиша мыши:
void CheckInt (int x, int y)
{
for (int i = 0; i < NUM_INT_ELEMENTS; ++i)
if (intTable[i] != NULL && intTable[i]->active == 1)
if (x > intTable[i]->x &&
x < intTable[i]->x+intTable[i]->width &&
y > intTable[i]->y &&
y < intTable[i]->y+intTable[i]->height)
IntProc(i);
}
Счётчик i "пробегает" по всем элементам таблицы интерфейса. Если элемент таблицы существует и он активен (обратите внимание, что видимость элемента не проверяется), то проверяется пересечение точки (позиции курсора) и прямоугольника (элемента интерфейса). Если пересечение произошло, вызывается функция IntProс, в которую передаётся i. В данном случае i - это одна из тех констант, которые мы определи ранее.
Процедура интерфейса
Итак, мы подошли к самой важной части функционирования нашего интерфейса - к функции IntProc (Interface Procedure). Эту функцию я назвал именно так по аналогии с WndProc. Эти функции очень похожи. Как мы знаем в WinProc обрабатываются сообщения окна. В процедуре интерфейса будут обрабатываться нажатия на активные элементы. Вместо идентификатора сообщений (как в WndProc) в IntProc проверяются элементы таблицы интерфейса, которые мы задали константами. Ещё раз хочу подчеркнуть, что процедура интерфейса будет вызываться, только если была нажата клавиша мышки (проверяется в основном цикле) и элемент интерфейса в позиции курсора оказался активным (проверяется в CheckInt). Посмотрим на код функции:
void IntProc(int element)
{
switch (element)
{
case SKIN: // обработку SKIN и MENU можно отсюда убрать
break; // так как эти элементы неактивны
case MENU:
break;
case GRID: // нажата кнопка сетки
if (gridFlag == 0)
gridFlag = 1;
else
gridFlag = 0;
break;
case MENU_BUTTON:
fsm = MENU_STATE;
for (int i = 0; i < NUM_INT_ELEMENTS; ++i)
{
if (intTable[i] != NULL && intTable[i]->parent == SKIN)
intTable[i]->active = 0;
if (intTable[i] != NULL && intTable[i]->parent == MENU)
{
intTable[i]->active = 1;
intTable[i]->visible = 1;
}
}
intTable[MENU]->visible = 1;
break;
case RETURN:
fsm = RUN;
for (int i = 0; i < NUM_INT_ELEMENTS; ++i)
{
if (intTable[i] != NULL && intTable[i]->parent == SKIN)
intTable[i]->active = 1;
if (intTable[i] != NULL && intTable[i]->parent == MENU)
{
intTable[i]->active = 0;
intTable[i]->visible = 0;
}
}
intTable[MENU]->visible = 0;
break;
case ERASE:
Erase();
break;
case EXIT:
PostQuitMessage(0);
break;
case TRIANGLE_POINTS:
fill = 0;
break;
case TRIANGLE_EDGES:
fill = 1;
break;
case TRIANGLE_FILLED:
fill = 2;
break;
}
}
Давайте разбираться. Здесь обрабатываются все элементы, хотя можно было бы убрать обработку неактивных элементов, так как для них функция никогда не будет вызвана.
GRID - данный элемент включает и выключает сетку (левая кнопка на панели инструментов). В 25-ом выпуске я советовал для обработки это кнопки использовать таймеры. Здесь они не нужны, так как нажатие левой кнопки мыши мы получаем (lmb = 1), когда пользователь отпускает клавишу.
gridFlag - глобальная переменная, которая проверяется после отрисовки тайлов. gridFlag = 1 - сетка рисуется, 0 - не рисуется.
MENU_BUTTON - обрабатывается при нажатии на кнопку "Меню" на панели инструментов (button - кнопка). Прежде всего здесь меняется конечный автомат fsm. Всего в программе два состояния: MENU и RUN. Проверка на нажатие плиток осуществляется. когда fsm = RUN. Далее проверяются все элементы таблицы интерфейса: те, у которых родительским элементом является SKIN, становятся неактивными (но видимыми), а те, у которых родительский элемент - MENU, становятся видимыми и активными. В самую последнюю очередь элемент MENU становится видимым.
RETURN - обрабатывается при нажатии кнопки "Вернуться" (return - возвращаться) в меню. Здесь происходит обратный процесс нажатия MENU_BUTTON: fsm присваивается RUN (теперь будет проверяться столкновение курсора и плиток при нажатии кнопки мыши), элементы SKIN становятся активными, а элементы MENU становятся невидимыми и неактивными.
ERASE - обрабатывается при нажатии на четвёртую кнопку на панели инструментов. При этом вызывается функция Erase (erase - стирать), в которой удаляются все треугольники.
EXIT - обрабатывается при нажатии на кнопку "Закрыть" в меню (exit - выход). При этом вызывается функция PostQuitMessage.
Последние три случая: TRIANGLE_POINTS (point - точка), TRIANGLE_EDGES (edge - ребро), TRIANGLE_FILLED (filled - залитый, закрашенный) - меняют переменную fill (fill - заливать). Это глобальная переменная, которая отвечает за способ вывода треугольников: 0 - треугольники выводятся точками, 1 - треугольники выводятся рёбрами, 2 - выводятся закрашенные треугольники.
Вот и всё. Обратите внимание, как легко теперь стало добавлять новые элементы интерфейса и их обработку: достаточно создать константу-индекс, выделить под элемент память, сохранить указатель в таблице интерфейса, проинициализировать поля класса и добавить обработку элемента в IntProc.
Вывод интерфейса на экран - функция DrawInterface
В конце основного цикла замыкается буфер (всё окно) и вызывается функция DrawInterface:
void DrawInterface()
{
intTable[SKIN]->DrawIntObject(lockedRect);
DrawTiles();
if (gridFlag == 1)
{
DrawGrid();
}
for (int i = 1; i < NUM_INT_ELEMENTS; ++i)
if (intTable[i] != NULL && intTable[i]->visible == 1)
intTable[i]->DrawIntObject(lockedRect);
}
При выводе интерфейса у нас возникает небольшая сложность. Мы не можем просто организовать цикл и вывести все элементы интерфейса. Дело в том, что поле клеток расположено над фоном (элемент SKIN). Поэтому здесь сначала выводится фон, затем плитки, сетка, а потом все остальные видимые элементы интерфейса.
Поэтому важно, чтобы SKIN был самым первым элементом, тогда остальные элементы мы можем вывести простым циклом. Функцию DrawTiles, которая рисует клетки, мы рассмотрим позже. Функцию подобную DrawGrid мы уже рассматривали в одном из предыдущих уроках.
lockedRect - указатель на замкнутый прямоугольник в буфере я сделал глобальным, он получает значение в основном цикле перед вызовом DrawInterface.
По интерфейсу всё. Не могу ещё раз не отметить простоту создания новых элементов. Подобный интерфейс уже можно использовать в простеньком реальном проекте.
Клетки v0.3
Теперь, когда мы разобрались с интерфейсом, приступим к рассмотрению новой версии клеток. В данный момент у нас уже есть полностью рабочий интерфейс, реагирующий на нажатие кнопки с сеткой, "Меню", "Вернуться", "Выход". Остальные кнопки обрабатываются, но их действия пока не видны.
В прошлом уроке мы выяснили, что после того, как вершины треугольников спроецировались в проекционную плоскость, они проецируются в конечную координатную плоскость экрана. Т.е. с этого момент координаты x,y вершин должны бить целыми и находиться на отрезках длиной в ширину/высоту окна. Вот с этого момента мы и начнём. Только вместо экрана наши вершины будут задаваться на плоскости тайлов. Т.е. мы будем работать не с пикселями, а с клетками. Это позволит нам увеличивать/уменьшать картинку.
Итак, у нас есть три вершины на конечной плоскости. Именно в этот момент видеокарта рисует между вершинами рёбра и закрашивает их.
Весь процесс преобразования вершин треугольников из бесконечной плоскости в конечную и дальнейшее рисование треугольников, называется растеризацией.
До растеризации треугольники идеальны - их координаты очень точные, а рёбра между треугольниками идеально ровные линии. После растеризации на треугольники накладываются ограничения нашего реального мира - координаты треугольников конечны (чтобы их можно было указать на экране монитора), а рёбра не совсем прямые, так как пиксели из которых они состоят, являются маленькими квадратами (а их размеры зависят от возможностей монитора).
С помощью программы клетки v0.3 мы узнаем как происходит растеризация треугольников.
Пользователь может щёлнкуть на поле с клетками. В этом месте создаётся вершина. При создании двух вершин рисуется линия, при создании трёх - треугольник.
Начнём с класса для треугольников:
class Triangle
{
public:
DWORD color;
int x1,y1,x2,y2,x3,y3;
Triangle ()
{
srand(timeGetTime());
color = 0;
color = (rand() % 255)*pow(2.0f,16);
color += (rand() % 255)*pow(2.0f,8);
color += rand() % 255;
x1 = -1;
y1 = -1;
x2 = -1;
y2 = -1;
x3 = -1;
y3 = -1;
}
void SortVertices();
};
Каждый треугольник имеет цвет (сравните с треугольниками в DirectX, где цвет определялся для каждой вершины) и три вершины. В конструкторе "создаётся" случайный цвет (pow - функция возведения в степень), а координатам вершин присваивается -1. Все вершины будут принадлежать полю клеток, а это значит, что корректные координаты задаются в отрезках [0,NUM_COLUMNS-1] по горизонтали и [0,NUM_ROWS-1] по вертикали. Инициализация всех вершин минус единицей позволяет нам сказать, что вершина ещё не создана на поле с клетками.
Метод SortVertices сортирует вершины треугольников. Первая вершина (x1,y1) становится верхней, а третья (x3,y3) - нижней. Соответственно, вторая вершина (x2,y2) расположена посередине. В сортировке используется несколько простых ветвлений. Зачем нужно сортировать вершины в треугольнике мы узнаем ниже.
Таблица треугольников
Все треугольники хранятся в таблице аналогичной таблице интерфейсов. Я назвал её objTable:
const int MAX_TRIANGLES = 8; Triangle* objTable[MAX_TRIANGLES]; int counter = 0;
Максимальное количество треугольников задаётся константой MAX_TRIANGLES.
В отличии от элементов интерфейса, каждый из которых выполнял свою задачу, все треугольники обрабатываются одинаково. Поэтому для треугольников нам не нужно создавать констант-индексов.
Переменная counter указывает на последний созданный треугольник (counter - счётчик). Она нужна нам для правильного создания всех трёх вершин в треугольнике и для проверки переполнения таблицы треугольников. Здесь же стоит упомянуть ещё о двух массивах:
int map[NUM_ROWS*NUM_COLUMNS]; // массив клеток int tiles[MAX_TRIANGLES+1][TILE_SIZE]; // типы клеток
map - всё поле клеток.
tiles - массив с отдельными тайлами. Здесь хранятся все типы тайлов используемые в программе. Тут стоит обратить внимание на два момента: Первый: размер одного тайла - TILE_SIZE - строка пикселей, а не квадрат (TILE_SIZE*TILE_SIZE). Мы используем строку пикселей, так как каждый тайл залит только одним цветом, а не текстурой. Можно было бы хранить только один пиксель, но при копировании тайла в фоновый буфер, тайл копируется построчно. Второй момент: размер массива тайлов - MAX_TRIANGLES+1. У каждого треугольника свой цвет. Т.е. на каждый треугольник нужен один тайл. Плюс нужен ещё один тайл для фонового (белого) цвета. Белый тайл создаётся в InitGraphics.
При запуске программы таблица объектов пуста. Обнуление всех указателей таблицы происходит в InitGraphics.
Основной цикл
При нажатии левой кнопки мыши, если fsm = RUN (меню не открыто), проверяется столкновение курсора с одним из тайлов:
if (fsm == RUN && lmb == 1)
{
for (int i = 0; i < NUM_ROWS; ++i)
for (int j = 0; j < NUM_COLUMNS; ++j)
{
top = OFFSET_Y + i*TILE_SIZE;
left = OFFSET_X + j*TILE_SIZE;
bottom = top + TILE_SIZE-1;
right = left + TILE_SIZE-1;
if (y >= top && y <= bottom &&
x >= left && x <= right)
NewVertice(j,i);
}
}
Если в момент, когда пользователь отпустил левую кнопку мыши, курсор был над одним из тайлов, вызывается функция NewVertice (new - новый, vertice - вершина), в которую передаются координаты тайла. Обратите внимание, это не координаты курсора, а координаты тайла в map.
Создание новой вершины
В функции NewVertice осуществляется несколько проверок. В этой функции x и y - это координаты тайла в map (а не курсора). Код приводить не буду.
1. Проверяется заполненность таблицы объектов.
2. Проверяется существование вершины в данных координатах. Если вершина уже создана, то новая не создаётся. Благодаря этому условию, все вершины всех треугольников имеют разные координаты.
3. Проверяется существование треугольника в текущей позиции (counter) таблицы. Если треугольника нет, то он создаётся. Здесь же происходит заливка тайла треугольника цветом.
4. Проверяется первая вершина текущего (counter) треугольника в таблице. Проверяется только x1 (y1 проверять не нужно). Именно здесь нам пригодилась инициализация минус единицей. -1 означает, что вершина ещё не создана. Если выполняется это условия, то x1,y1 присваиваются параметры функции (координаты тайла в map).
5. Проверяется существование второй вершины (также с помощью проверки на -1).
6. Проверяется существование третьей вершины. Обратите внимание, что именно в теле этого условия увеличивается counter - теперь можно создавать новый треугольник, так как заполнены все три вершины текущего.
Вот и всё. Эта функция позволяет нам заполнить таблицу объектов. Теперь нужно эти треугольники вывести на экран. Это происходит в функции DrawTiles, которая вызывается при отрисовке интерфейса.
Вывод тайлов
В начале функции DrawTiles вызывается функция Clear. В этой функции происходит очистка поля фоновым тайлом (белый цвет). Функцию Clear необходимо вызывать, чтобы корректно происходила смена режимов заливки (fill).
Оставшаяся часть функции DrawTiles разделена на две части: в первой треугольники рисуются в map, во второй map выводится на экран. На второй части мы останавливаться не будем, она почти такая же, как в 25-ом выпуске. Что касается заполнения map треугольниками. Счётчик i пробегает по всем элементам таблицы объектов. Если какой-то из элементов таблицы не существует, он пропускается.
После этого координаты треугольника записываются во временные, для того чтобы меньше печатать:
int x1,y1,x2,y2,x3,y3; x1 = objTable[i]->x1; y1 = objTable[i]->y1; x2 = objTable[i]->x2; y2 = objTable[i]->y2; x3 = objTable[i]->x3; y3 = objTable[i]->y3;
Затем проверяется глобальная переменная fill, которая меняет значение тремя кнопками в панели инструментов. 0 - треугольник выводится в map вершинами, 1 - в map рисуются рёбра треугольника, 2 - в map рисуется закрашенный треугольник. Здесь я объясню случай 2, так как он включает и оба предыдущих:
case 2:
// рисование точек
if (x1 != -1)
map[x1+NUM_COLUMNS*y1] = i+1;
if (x2 != -1)
map[x2+NUM_COLUMNS*y2] = i+1;
if (x3 != -1)
map[x3+NUM_COLUMNS*y3] = i+1;
// рисование линий
if (x1 != -1 && x2 != -1)
DrawLine(x1,y1,x2,y2,i);
if (x2 != -1 && x3 != -1)
{
DrawLine(x2,y2,x3,y3,i);
DrawLine(x3,y3,x1,y1,i);
}
// рисование треугольника
if (x3 != -1)
DrawTriangle(objTable[i],i);
break;
Сначала в map рисуются вершины (если вершины определены - не равны -1). Затем рисуются рёбра треугольника. Рёбра рисуются только между существующими вершинами. Рисование линий осуществляется функцией DrawLine. Первые четыре параметра - координаты концов отрезка, пятый - индекс треугольника/тайла.
Если определена третья вершина треугольника, то треугольник закрашивается. Заливка треугольника происходит в функции DrawTriangle. Первый параметр - указатель на треугольник, который будет рисоваться, второй - индекс треугольника/тайла.
И напоследок небольшое замечание: при присваивании элементу map тайла треугольника, используется индекс этого треугольника из таблицы объектов увеличенный на единицу. Это необходимо из-за того, что нулевой тайл в массиве tiles - фоновый. Если вы хотите убрать из вычислений прибавление единицы, то фоновый тайл сделайте последним в tiles (в функции InitGraphics).
Алгоритм Брезенхема
Для растеризации отрезков мы воспользуемся алгоритмом Брезенхема, который был разработан для плоттеров в начале шестидесятых.
В функцию DrawLine передаются координаты концов отрезка.
Сначала нужно выделить частные случаи: когда прямая параллельна одной из осей:
int dx = x2 - x1;
int dy = y2 - y1;
if (dx == 0)
{
if (dy > 0)
for (int i = y1 + 1; i < y2; ++i)
map[x1+i*NUM_COLUMNS] = tile+1;
else
for (int i = y1 - 1; i > y2; --i)
map[x1+i*NUM_COLUMNS] = tile+1;
return;
}
float k;
k = static_cast(dy)/static_cast(dx);
if (k == 0)
{
if (dx > 0)
for (int i = x1 + 1; i < x2; ++i)
map[i+y1*NUM_COLUMNS] = tile+1;
else
for (int i = x1 - 1; i > x2; --i)
map[i+y1*NUM_COLUMNS] = tile+1;
return;
}
Сначала находятся dx и dy. Если dx == 0, то прямая параллельна оси y. При этом нужно учесть два случая, когда dy > 0 и dy < 0. tile - индекс треугольника в таблице объектов, который передаётся в функцию (пятый параметр). Если прямая не параллельна y, то можно посчитать угловой коэффициент. Если отрезок параллелен оси x (k==0), то в зависимости от dx выводится горизонтальная линия.
В алгоритме Брезенхема для нахождения неизвестных координат не используется уравнение прямой. Но при этом нужно определить какое значение растёт быстрее: x (прямая пологая) или y (прямая крутая). Для этого нужно проверить значение углового коэффициента.
Если x растёт быстрее y, то k будет больше нуля, но меньше 1 (в коде мы сразу обрабатываем и отрицательный коэффициент). Так вот, в таком случае нужно организовать цикл по x, а значение y вычислять с помощью k:
if (k > 0 && k <= 1 || k < 0 && k >= -1)
{
float y = y1;
if (dx > 0)
for (int i = x1+1; i < x2; ++i)
{
y += k;
map[i+static_cast(y)*NUM_COLUMNS] = tile+1;
}
else
for (int i = x1-1; i > x2; --i)
{
y -= k;
map[i+static_cast(y)*NUM_COLUMNS] = tile+1;
}
}
Рассмотрим первую ветвь, где dx больше нуля. Счётчик i пробегает все значения от x1, до x2. Каждую итерацию цикла y увеличивается на k. Рассмотрим конкретный пример: x1 = 0, x2 = 10, y1 = 0, y2 = 5, k = 5/10 = 0,5. Т.е. x растёт в два раза быстрей, чем y. Вот как для этих значений будет выполняться предыдущий цикл:
i = 1; y = 0,5 i = 2; y = 1 i = 3; y = 1,5 i = 4; y = 2 i = 5; y = 2,5 i = 6; y = 3 i = 7; y = 3,5 i = 8; y = 4 i = 9; y = 4,5
В результате будет нарисована прямая с точками: (1,0),(2,1),(3,1),(4,2),(5,2),(6,3),(7,3),(8,4),(9,4). Заметьте, точки (0,0) и (10,5) нарисованы не будут. Можно изменить условия цикла, но нам это не нужно - эти точки автоматически рисуются в DrawTiles.
Что если бы в данном примере i пробегал по значениям y? Половина точек не была бы нарисована. Именно поэтому в алгоритме Брезенхема определяется,s какая координата растёт быстрее.
В данном случае дробная часть просто отбрасывается (стандартное поведение C++). Чтобы линия была нарисована точнее (к своему уравнению), координату, которая растёт медленнее, можно округлять. Я не стал этого делать, чтобы код выглядел проще.
Кстати, заметьте, что здесь же мы обрабатываем и случай, когда x и y растут с одинаковой скоростью (k=1). Этот случай не важно где рассматривать, я вставил его сюда.
Второй случай: y растёт быстрее x (прямая крутая). Коэффициент будет больше единицы. Обратите внимание, что для увеличения (или уменьшения) x используется k-1. До цикла можно было бы создать временную переменную, чтобы деление на k не происходило каждую итерацию.
if (k > 1 || k < -1)
{
float x = x1;
if (dy > 0)
for (int i = y1+1; i < y2; ++i)
{
x += 1/k;
map[static_cast(x)+i*NUM_COLUMNS] = tile+1;
}
else
for (int i = y1-1; i > y2; --i)
{
x -= 1/k;
map[static_cast(x)+i*NUM_COLUMNS] = tile+1;
}
}
По растеризации линий всё. Ещё раз хочу обратить внимание, что линии можно сделать более "точными", если округлять значения координаты, растущей медленнее.
Заливка треугольников
Последний метод! Он трудный самый!
Начнём с кода DrawTriangle. Функция принимает указатель на Triangle - tri и индекс этого треугольника в таблице - tile:
tri->SortVertices(); int x1 = tri->x1; int y1 = tri->y1; int x2 = tri->x2; int y2 = tri->y2; int x3 = tri->x3; int y3 = tri->y3; float dx12,dx13,dx23,dy12,dy13,dy23; dx12 = x2-x1; dy12 = y2 - y1; dx13 = x3-x1; dy13 = y3 - y1; dx23 = x3-x2; dy23 = y3 - y2;
Сначала в функции вызывается метод сортировки вершин треугольника. Этот метод можно (и нужно) вызывать при создании третьей вершины в функции NewVertice, так как сортировать вершины нужно только один раз. здесь же метод сортировки вызывается каждый кадр. Ну да ладно.
Далее для сокращения кода координаты вершин присваиваются временным переменным. Затем находим dx и dy трёх отрезков.
Без сортировки вершин было бы проблематично построить треугольник. В результате сортировки y1 (первой вершины) - самый верхний, y3 (третьей вершины) - самый нижний, а вторая вершина находится посередине. Для краткости будем обращаться к вершинам как 1, 2, 3. Отрезок 13 - самый длинный по высоте. Возможны ситуации, когда y1 == y2 (12 - верхнее ребро параллельное оси x), y2 = y3 (13 - нижнее ребро параллельное оси x) и y1 == y2 == y3 (треугольника нет, есть прямая линия параллельная оси x). Мы можем сразу учесть этот случай. В функции он обрабатывается так:
if (dy13 == 0) return;
Т.е. если y1 == y3, происходит выход из функции.
Для всех остальных случаев нужно пробегать все значения по y на отрезке 13 (самый длинный отрезок по высоте). Пусть это будет счётчик i. При этом треугольник будет закрашиваться построчно: сверху вниз. Чтобы знать, какие пиксели закрашивать нужно находить неизвестные x Для двух рёбер и рисовать между ними прямую параллельную оси x. Возможны два случая: i >= y2, тогда нам нужны уравнения двух линий: 12, 13 и i < y2, тогда будут находиться значения x отрезков 13 и 23.
Так как отсчёт счётчика начнётся с y1. То Оба неизвестных икса (отрезков 12 и 13) примут значения x1. Неизвестные x двух отрезков я назвал в коде как a, b:
float a=x1,b=x1;
Далее начинается цикл по всем y на отрезке 13:
for (int i = y1; i <= y3; ++i)
{
Как я писал выше, мы пробегаем по всем y на отрезке 13. Далее нужно учесть частные случаи: когда отрезок 12 образует верхнее ребро параллельное оси x, когда отрезок 23 образует нижнее ребро параллельное оси x. В этих случаях, мы просто пропускаем итерацию цикла:
if (y2 == y3 && y3 == i || y1 == y2 && y1 == i)
continue;
Теперь давайте вспомним уравнение прямой прохо