Вступление

Дата создания: 2009-01-22 00:00:57
Последний раз редактировалось: 2012-02-08 08:43:58

Это первый урок из раздела Математика. Надеюсь мы закончим вводный курс к моменту начала публикации в рассылке выпусков по directX. Вполне вероятно, что получится закончить математический вводный курс гораздо раньше: тем не слишком много и они не сказать чтобы сложные. Приступим.

Координатные пространства

В большинстве примеров будет использоваться трёхмерное координатное пространство. Возможны два варианта трёхмерного пространства: ось z уходит вглубь листа и наоборот. Это продемонстрировано на рис. 1.

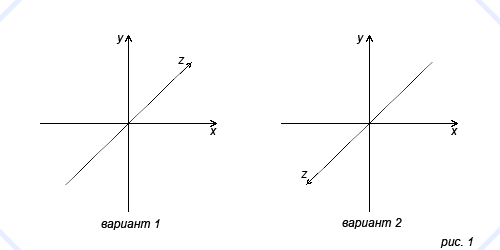
Мы всегда будем пользоваться первым. Выбор этот не произвольный. Дело в том, что как раз такое представление пространства используется в DirectX. А вот если бы мы использовали OpenGL, тогда бы выбрали второй вариант.

Расстояние между двумя точками

В начале рассмотрим самый простой случай - точка на координатной прямой (рис.2а). Расстоянием до точки M от начала координат будет значение координаты данной точки - x. Для кракткости используют форму - M(x).

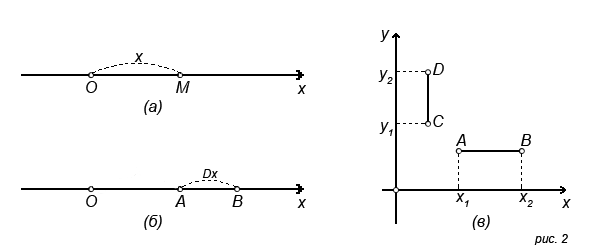
рис.2б: на координатной прямой заданы две точки А и B с координатами x₁, x₂ - A(x1), B(x₂). Расстояние между ними можно найти вычтя значение второй координаты из первой.

Dx = x₂ - x₁

Здесь Dx - расстояние между двумя точками, которое в математике обычно обозначается Δx, где Δ читается как - дельта.

рис.2в: мы добавили ещё одну ось. Здесь рассматривается случай, когда отрезки между точками параллельны осям. На плоскости заданы четыре точки: A(x₁,y₃), B(x₂,y₃), C(x₃,y₁), D(x₃,y₂)

Расстояниями между точками будут:

Dx = x₂ - x₁ Dy = y₂ - y₁

Теперь рассмотрим ситуацию когда отрезок проведённый между двумя точками не параллелен осям координат - рис.3:

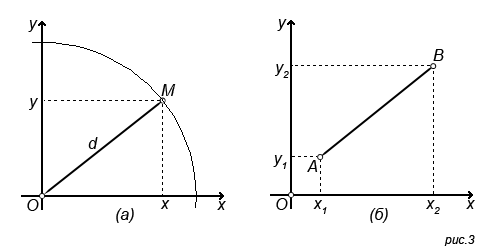
Здесь, на координатной плоскости задана точка M(x,y), где x, y имеют конкретные значения, возможно: x = 5, y = 4.

Расстояние между точками O(0,0), M(x,y) находится по теореме Пифагора из прямоугольного треугольника, где d - гипотенуза, а x, y - катеты.

d² = x² + y²

Если первая точка находится не в начале координат (рис.3б), то формула нахождения расстояния между точками A(₁,y₁), B(x₂,y₂) следующая:

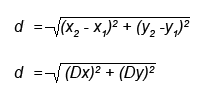
Ну и последний случай, две точки расположены в пространстве (рис.4). Их координаты - A(x1,y1,z1), B(x2,y2,z2). Небольшое замечание: соответствуюище координаты имеют названия. x - абсцисса точки, y - ордината, z - аппликата. Координаты точки - упорядочены. Это значит, что нелья менять их местами и всегда нужно записывать сначала x, затем y и только потом z.

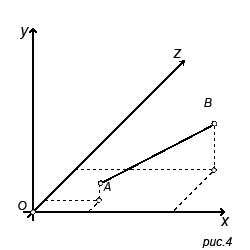
Прежде чем спроецировать координаты на оси, нужно опустить перпендикуляр на соответствующую плоскость. На рисунке, из точек опускается перпендикуляр на плоскость xz. Ординаты (y1 и y2) точек в данном случае - это перпендикуляры опущенные из соответствующих точек на плоскость xz.

Формула для нахождения расстояния между точками в пространстве мало отличается от формулы для нахождения расстояния между точками на плоскости:

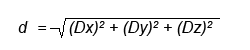
Дополнительное упражнение к пятому выпуску рассылки

Для данного упражнения вам понадобится включить заголовочный файл math.h.

Напишите программу, где пользователь вводит координаты, куда нужно переместить обьект. Программа подсчитывает расстояние на которое переместился пользователь. Для хранения расстояния используйте отдельную переменную.

Пользователь вводит координаты через запятую: 12,21,3.4.

Заметьте, что в английском, используется десятичная точка, а не запятая. Поэтому следующий оператор присвоит переменной 0, а не 0.5:
float x = 0,5; // нужно записать: float x = 0.5
Использование запятой вместо точки может стать причиной труднообнаруживаемых ошибок.

Операция извлечения (>>) может считывать больше одного значения за раз. Для этого вам понадобится определить переменную типа char, например - helper:
cin >> a >> helper >> b;

Переменные x1,y1,z1,x2,y2,z2 - типа float. После того как пользователь ввёл новые значения, Вы находите расстояние между старой точкой и новой и добавляете к переменной хранящей расстояние. Затем присваиваете старой точке координаты которые ввёл пользователь.

Для нахождения корня квадратного используйте фукнцию sqrt(). В скобки вставьте выражение, чей квадратный корень вам нужно найти: d = d + sqrt(Dx*Dx + Dy*....).

Если возникнут вопросы или сложности с выполнением задания пишите мне e-mail. Попытаемся разобраться.