Внимание! Данный сайт не обновляется. Новая версия: shatalov.su

Прямая линия

Дата создания: 2010-03-20 14:57:17
Последний раз редактировалось: 2012-02-08 08:49:02

Прямые линии довольно ограниченно используются в компьютерной графике. Тем не менее, необходимо хорошо представлять как прямые определяются в математике.

Для начала нужно выделить самое важное. Для этого давайте посмотрим на картинку:

Замечание
На картинках и в тексте для обозначения угла используется alpha, а для обозначения числа Пи - Pi. Правильнеё было бы использовать буквы греческого алфавита, но существуют проблемы с их вставкой в текст, поэтому греческие буквы я использовал только в формулах (конец урока).
Буква альфа в греческом алфавите выглядит вот так: Α - заглавная, α - строчная.
Буква Pi: Π - заглавная, π - строчная.

Прямые линии задаются всего двумя параметрами:
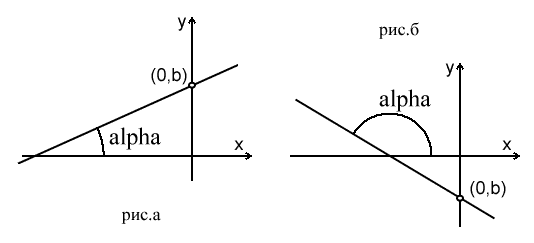
1. Углом между прямой и положительным направлением оси x. На картинке это угол alpha.
2. Точкой пересечения прямой с осью y. Так как абсцисса этой точки всегда будет равна нулю, то можно выделить ординату. На картинке это переменная b.

Угол alpha определяет наклон (slope) прямой. Меняя этот угол можно задать прямые с разным наклоном. Меняя значение b можно передвигать прямую вверх/вниз.

На рисунке а угол alpha меньше девяноста градусов - прямая образует с осью x острый угол, на рисунке б угол alpha больше девяноста градусов - прямая образует с осью x тупой угол.

Угол alpha может принимать следующие значения: [0, Pi] - от нуля до 180 градусов. Диапазон значений угла можно записать ещё вот так: 0 <= alpha <= Pi. Напоминаю, что 180 градусов в радианной мере угла равно числу Pi (3,14).

При b = 0, прямая будет проходить через начало координат.

Прежде чем мы начнём обсуждать уравнение прямой, стоит взглянуть на два частных случая: прямые параллельные оси x и прямые параллельные оси y:

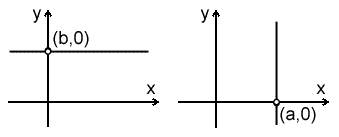
Если прямая параллельна оси x, то её можно задать с помощью ординаты точки пересечения прямой с осью y - b, угол alpha будет равен нулю. Если прямая параллельна оси y, то её можно задать с помощью абсциссы точки пересечения прямой с осью x - a, угол alpha будет равен 90 градусам - Pi/2.

Уравнения прямой с угловым коэффициентом

Теперь, когда мы знаем от каких параметров зависит прямая, мы можем составить уравнение прямой. Существует несколько форм этого уравнения. Сначала мы рассмотрим уравнение прямой с угловым коэффициентом.

Зачем вообще нужно уравнение прямой? С помощью уравнения можно, например, узнать, лежит ли произвольная точка плоскости на прямой. Но самое главное, зная уравнение прямой, можно построить эту прямую, например, на экране монитора.

На данный момент у нас есть две величины: угол наклона и ордината точки пересечения прямой с осью y. Нам нужно как-то избавиться от угла и привести оба параметра к одной системе измерения. Т.е. угол нужно выразить в тех же величинах, что и параметр b. Сделать это можно с помощью тригонометрических функций: синуса, косинуса, тангенса и котангенса. Как мы знаем, эти функции можно выразить с помощью сторон прямоугольного треугольника. Соответственно, теперь нам нужен прямоугольный треугольник. Рассмотрим немного изменённую первую картинку:

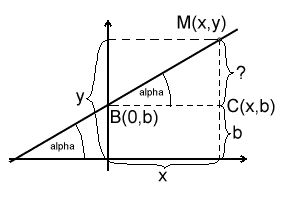
М - произвольная точка на прямой. Здесь мы отчётливо видим прямоугольный треугольник. У нас есть две неизвестные координаты: x, y и два параметра: угол alpha и b. Нам осталось составить функцию: выразить y через всё остальное. Значение y равно b плюс катет прямоугольного треугольника, который на рисунке показан знаком вопроса.

Стало быть, теперь нам нужно найти неизвестный катет. Основная задача здесь - избавиться от гипотенузы в уравнениях. Для этого нам понадобится несколько формул:

Сначала нужно выразить неизвестный катет через уравнение синуса.
```
sin(α) = MC/MB    // MB - гипотенуза
MC = MB * sin(α)
```
Затем выражаем синус угла через тангенс:
```
tg(α) = sin(α)/cos(α)
sin(α) = tg(α) * cos(α)
```
Затем выражаем гипотенузу через косинус и известный катет:
```
cos(α) = BC/MB = x/MB
MB = x / cos(α)
```
И наконец, в формулу из первого пункта подставляем значение синуса из второго и значение MB из третьего:
```
MC = ( x / cos(α) ) * ( tg(α) * cos(α) ) = x * tg(α)
```

Это мы получили MC. Чтобы получить y произвольной точки (в нашем случае - точки M), к MC необходимо прибавить b:

y = tg(α)*x + b

Заменим в этом уравнении tg(alpha) на k: k = tg(alpha). k - угловой коэффициент прямой. В итоге у нас получится уравнение прямой с угловым коэффициентом:

y = k*x + b

В данном уравнении значения x и y зависят от двух параметров: b - ординаты точки пересечения прямой с осью y и k - угловым коэффициентом. При этом k = tg(alpha). Соответственно, прямая (её наклон) зависят от k. Вот мы и пришли к тому, с чего начинали: прямая зависит от b и угла. Только в уравнении с угловым коэффициентом угол представлен тангенсом.

Вернёмся к двум частным случаям: если прямая параллельна оси x, то так как tg(0) = 0, уравнение с угловым коэффициентом будет выглядеть вот так:

y = b

Если прямая параллельна оси y, то tg(90) неопределён, так как tg(a) = sin(a)/cos(a), sin(90) = 1, cos(90) = 0, а на ноль делить нельзя. Уравнение прямой в данном случае записывается вот так:

x = a

Где a - абсцисса точки пересечения прямой с осью x (смотрите вторую картинку).

И последнее. Как определить наклон прямой по значению углового коэффициента: если k > 0, то угол между прямой и положительным направлением оси x - острый, если k < 0, угол тупой.

На сегодня всё.

Позже добавлю уравнение прямой, проходящей через две точки, уравнение прямой, проходящей через данную точку в заданном направлении и кое-что ещё.