Матрицы

Дата создания: 2009-04-23 10:20:06
Последний раз редактировалось: 2012-02-08 09:07:25

Есть такая шутка про определение матриц:

Матрица - это прямоугольная таблица чисел. Единственная проблема с данным определением, что это не таблица, она не прямоугольная и не чисел.

Но вообще, это удобно рассматривать матрицу в видет прямоугольной таблицы чисел.

Матрица представляет из себя таблицу чисел размером mxn, где первое число m - количество строк, а второе n - количество столбцов. Это нужно запомнить: первое число - строка, второе число - столбец.

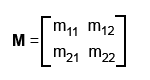
Здесь мы видим матрицу из четырёх элементов. Размер данной матрицы 2x2 - две строки и два столбца.

Матрицы по многим свойствам аналогичны векторам и с помощью матрицы можно представить вектор, только у них есть ряд дополнительных возможностей.

Матрицы одна из самых главных тем математики в играх. С помощью матриц производятся линейные преобразования, что позволяет управлять объектами в пространстве.

Операции над матрицами

В примерах данной статьи мы будем использовать следующие четыре матрицы:

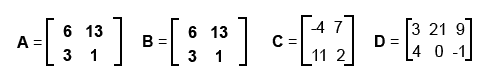
Некоторые операции над матрицами очень похожи на операции над векторами.

Равенство матриц

Две матрицы равны когда они одного размера и все их элементы совпадают.

A = B

Умножение матрицы на число

При умножении матрицы на число, все элементы перемножаются с этим числом.

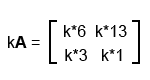
Сложение и вычитание матриц

Для вычисления суммы двух матриц, необходимо сложить соответствующие элементы этих матриц. Понятно, что при этом матрицы должны быть одного размера.

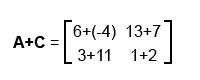
Разность матриц вычисляется аналогично.

Произведение матриц

Пожалуй самая интересная операция - умножени двух матриц.

Обязательное условие - количество столбцов первой матрицы должно совпадать с количеством строк второй.

Например у нас есть две матрицы размером: mxn и nxp. Вот эти две матрицы можно перемножать - количество столбцов первой матрицы равно количеству строк второй (число n). В результате перемножения двух матрицы мы получим матрицу размером mxp.

Рассмотрим произведение двух матриц K размером 4x3 и T размером 3x5. Найдём элемент 3x4 (находящийся в третьей строке и четвёртом столбце).

Каждый элемент матрицы вычисляется следующим образом: из первой матрицы берётся строка, номер которой совпадает с номером строки элемента, который мы вычисляем. То есть из первой матрицы берём все элементы из третьей строки. Из второй матрицы берутся элементы столбца, номер которого совпадает с номером столбца элемента, который мы вычисляем. Т.е. все элементы четвёртого столбца из второй матрицы. Обратите внимание что и из первой и из второй матрицы мы взяли одинаковое количество элементов (три).

Вот какие элементы мы взяли:

Из первой матрицы: k₃₁, k₃₂, k₃₃ - все элементы третьей строки.

Из второй матрицы: t₁₄, t₂₄, t₃₄ - все элементы четвёртого столбца.

Теперь находим элемент матрицы P=KT:

p₃₄ = k₃₁*t₁₄ + k₃₂*t₂₄ + k₃₃*t₃₄

Обратите внимание, что мы нашли только один элемент! Все остальные элементы находятся аналогично.

Произведение матриц BD будем выглядеть следующим образом:

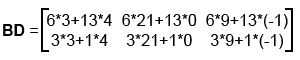
Для закрепления материала возьмите две матрицы размером 5x4 и 4x3. Заполните эти матрицы числам. Сначала найдите произведение матрицы в форме индексов, затем вместо индексов подставьте соответствующие числа матриц. Если Вы в первый раз слышите о матрицах, то сделать всё это просто необходимо! Причём нужно сделать это не в уме :), а взять листок бумаги и карандаш, и всё подробно расписать.

Единичные матрицы

Единичная матрица - это квадратная (матрица у которой количество строк равно количеству столбцов) матрица на главной диагонали которой расположены единицы, а все остальные элементы равны нулю.

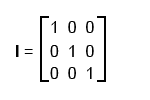
Транспонирование матриц

При транспонировании матрицы необходимо поменять местами строки и столбцы.

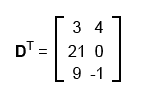
Представление векторов в матрицах

Векторы можно представлять в виде матриц. Например у нас есть вектор v = <x,y,z>. Его можно представить в виде матрицы: V = [ x y z ]. То есть это матрица с одной строкой. Ниже на картинке представлена матрица содержащая три вектора.

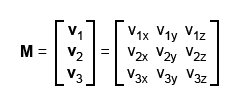
Данную матрицу можно записать в виде строки: M^T = [ v₁ v₂ v₃ ]. При этом, каждый вектор представлен столбцом.

---

Важно!!! Тема очень важная, нужно хорошо понимать материал. Поэтому если что-то непонятно по теме, то пожалуйста напишите мне на e-mail (ну или оставьте комментарий в одной из тем блога), что именно непонятно и что вызывает затруднения. Тогда я смогу сделать материал более доступным. Спасибо.