Тригонометрия

Дата создания: 2009-10-07 13:58:16
Последний раз редактировалось: 2012-02-08 09:15:56

Тригонометрия - это такое сложное греческое слово: тригонон - треугольник, метро - мерять. Стало быть по-гречески это означает: меряться треугольниками. Очень странное слово. Может быть древнегреки под треугольниками подразумевали кое-что другое? Не знаю. Но наверняка могу утверждать, что Задорнову, Драгункину и Фоменко нужно тщательнее изучить этот вопрос.

В общем, всё что связано с треугольниками, это и есть тригонометрия.

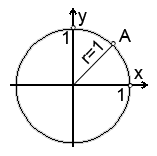
Мы будем рассматривать окружности с радиусом в одну единицу (единичную окружность). Пример такой окружности можно увидеть на картинке сверху. В чём измеряются эти самые единицы нам без разницы: в сантиметрах, метрах, дюймах, вёрстах. Если вам удобней, считайте что в тексте рассматривается окружность с радиусом в один метр.

Радианная мера угла

Как вы конечно же знаете, углы измеряются в градусах. Градусная мера понимается на интуитивном уровне (начиная с начальных классов): 180 градусов - смена направления, 90 градусов - поворот налево/направо.

Но в математике (и конечно же в компьютерных вычислениях) углы гораздо удобнее выражать в числах. Для этого и предназначена радианная мера угла.

Угол в один радиан

В школе даётся только несколь углов: 45г = Pi/4рад, 60г = Pi/3рад, 30г = Pi/6рад, и самые важные углы: 90г = Pi/2 и 180г = Piрад.

Как мы знаем, число Pi = 3,14. Соответственно угол в 180 градусов равен 3,14 радиан.

Давайте теперь научимся преобразовывать значения любых углов между градусной и радианной мерой. Возьмём два угла: a - угол измеряемый в градусах, b - угол измеряемый в радианах. Вот так выглядит формула преобразования из радианной меры в градусную:

a = b*180/Pi

А вот это формула преобразования из градусной меры в радианную:

b = a*Pi/180

Ну а чтобы совсем разобраться с радианами, рассмотрим картинку:

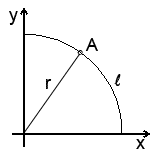
На картинке мы видим угол в один радиан (это примерно 57 градусов). На рисунке также обозначен радиус окружности (в нашем случае - 1) и дуга l (эль), образованной точками (1,0) и A. Так вот, радианная мера - это соотношение дуги к радиусу. Возьмём угол a (альфа), образованный положительным направлением оси Ox и радиусом. Вот как считается радианная мера этого угла:

a = l/r

При длине дуги в одну единицу (не забывайте, мы рассматриваем единичную окружность, поэтому r=1), мы получаем угол в один радиан.

Косинус и синус угла

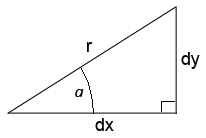
На рисунке заданы: угол a (альфа), r - гипотенуза, dx и dy - катеты. С помощью катетов и гипотенузы прямоугольного треугольника можно ввести понятие синуса и косинуса угла a.

Синус угла - это отношение противолежащего катета dy к гипотенузе r:

sin(a) = dy/r

Косинус угла - отношение прилежащего катета dx к гипотенузе r:

cos(a) = dx/r

Рассмотрим ещё один рисунок:

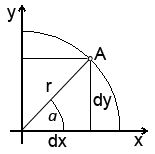
Как видите, здесь мы спроецировали координаты точки A на оси. Теперь у нас есть угол a (альфа) и прямоугольный треугольник образованный сторонами r,dx,dy.

Напоминаю, что мы рассматриваем окружность единичного радиуса. И мы конечно же воспользуемся этим важным свойством. Так как r = 1, мы получаем следующие формулы:

dx = cos(a)/r = cos(a)
dy = sin(a)/r = sin(a)

Использование трёх величин: dx,dy и a (и r, если r не равен 1), открывает перед нами потрясающие возможности.

Тангенс и котангенс угла

Подробно на тангенсе и котангсе мы останавливаться не будем. Посмотрим только на формулы:

tg(a) = sin(a)/cos(a)
ctg(a) = cos(a)/sin(a)

Т.е. тангенс угла - это отношение синуса к косинусу, а котангенс угла - отношение косинуса к синусу.

В C++ имена функций котангенса и тангенса не совпадают с обозначенями в наших учебниках по математике. Имя функции тангенса - tan, котангенса - cot.

Вот в общем-то и всё по тригонометрии. Этот материал можно сразу заучивать. Всё остальное - детали.