Векторы в компьютерных играх

Дата создания: 2009-04-11 15:25:51
Последний раз редактировалось: 2012-02-08 09:19:45

Долго я не хотел писать данную статью - думал как подавать материал. Ещё и картинки нужно рисовать. Но, видать сегодня удачно сложились звёзды и статье про векторы быть. Хотя, это всего лишь черновой вариант. В будущем данную статью разобью на несколько отдельных - материала достаточно. Также, постепенно статья будет улучшаться: буду вносить в неё изменения - т.к. за один присест не получится раскрыть все аспекты.

Векторы были введены в математику в девятнадцатом века, для описания величин, которые трудно было описывать с помощью скалярных значений.

Векторы интенсивно применяются при разработке компьютерных игр. Применяются они не только традиционно - для описания таких величин как сила или скорость, но и в областях, которые казалось бы никак не связаны с векторами: хранение цвета, создание теней.

Скаляры и векторы

Для начала напомню, что такое скаляр, и чем он отличается от вектора.

Скалярные значения хранят какую-то величину: масса, объём. То есть это сущность, которая характеризуется только одним числом (например, количество чего-либо).

Вектор в отличии от скаляра описывается с помощью двух значений: величина и направление.

Важное отличие векторов от координат: векторы не привязаны к конкретному местоположению! Ещё раз повторюсь, главное в векторе - длина и направление.

Вектор обозначается жирной буквой латинского алфавита. Например: a, b, v.

На первом рисунке можно увидеть как вектор обозначают на плоскости.

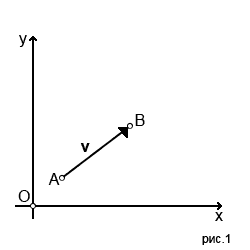
Векторы в пространстве

В пространстве векторы можно выражать с помощью координат. Но прежде нужно ввести одно понятие:

Радиус-вектор точки

Возьмём в пространстве какую-нибудь точку M(2,1). Радиус-вектор точки - это вектор начинающийся в начале координат и заканчивающийся в точке.

У нас здесь ни что иное как вектор OM. Координаты начала вектора (0,0), координаты конца (2,1). Обозначима этот вектор как a.

В данном случае вектор можно записать следующим образом a = <2, 1>. Это координатная форма вектора a.

Координаты вектора называются его компонентами относительно осей. Напрмер, 2 - компонета вектора a относительно оси x.

Давайте ещё раз остановимся на том, что такое координаты точки. Координата точки (например x) - это проекция точки на ось, т.е. основание перпендикуляра, опущенного из точки на ось. В нашем примере 2.

Но вернёмся к первому рисунку. У нас здесь две точки A и B. Пусть координатами точек будут (1,1) и (3,3). Вектор v в данном случае можно обозначить так v = <3-1, 3-1>. Вектор лежащий в двух точках трёхмерного пространстве будет выглядеть так:

v = <x₂-x₁, y₂-y₁, z₂-z₁>

Думаю никаких сложностей тут нет.

Умножение вектора на скаляр

Вектор можно умножать на скалярные значения:

kv = <k*v_x, k*v_y> = <k*2, k*1>

Здесь и далее, * - знак умножения.

При этом скалярное значение перемножается с каждой компонентой вектора.

Если k > 1, то вектор увеличится, если k меньше единицы, но больше нуля - вектор уменьшится в длину. Если же k меньше нуля, то вектор поменяет направление.

Единичные векторы

Единичные векторы - это векторы длина которых равна единице. Заметьте, вектор с координатами <1,1,1> не будет равным единице! Нахождение длины вектора описано ниже по тексту.

Существуют так называемые орты - это единичные векторы, которые по направлению совпадают с осями координат. i - орт оси x, j - орт оси y, k - орт оси z.

При этом i = <1,0,0>, j = <0,1,0>, k = <0,0,1>.

Теперь мы знаем что такое умножение вектора на скаляр и что такое единичные векторы. Теперь мы можем записать v в векторной форме.

v = v_xi + v_yj + v_zk, где v_x, v_y, v_z - соответствующие компоненты вектора

Сложение векторов

Чтобы полностью разобраться в предыдущей формуле необходимо понять, как работает сложение векторов.

Тут всё просто. Возьмём два вектора v1 = <x₁,y₁,z₁> и v₂ = <x₂,y₂,z₂>

v₁ + v₂ = <x₁+x₂, y₁+y₂, z₁+z₂>

Мы всего лишь складываем соответствующие компоненты двух векторов.

Разность вычисляется так же.

Это, что касается математической формы. Для полноты, стоит рассмотреть как будет выглядеть сложение и вычитание векторов графически.

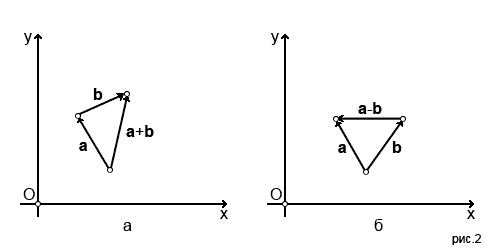
Для того, чтобы сложить два вектора a+b. Нужно совместить начало вектора b и конец вектора a. Затем, между началом вектора a и концом вектора b провести новый вектор. Для наглядности смотрите второй рисунок (буква "а").

Для вычитания векторов нужно совместить начала двух векторов и провести новый вектор из конца второго вектора к концу первого. На втором рисунке (буква "б") показано как оно выглядит.

Длина и направление вектора

Сначала рассмотрим длину.

Длина - это числовое значение вектора, без учёта направления.

Длина определяется по формуле (для трёхмерного вектора):

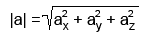
корень квадратный из суммы квадратов компонент вектора.

Знакомая формула, не правда ли? В общем-то - это формула длины отрезка

Направление вектора определяется по направляющим косинусам углов образованных между вектором и осями координат. Для нахождения направляющих косинусов используются соответствующие компоненты и длина (картинка будет позже).

Представление векторов в программах

Представлять векторы в программах можно различными способами. Как с помощью обычных переменных, что не эффективно, так и с помощью массивов, классов и структур.

float vector3[3] = {1,2,3}; // массив для хранения вектора

struct vector3 // структура для хранения векторов
{
  float x,y,z;
};

Самые большие возможности при хранении векторов нам предоставляют классы. В классах мы можем описать не только сам вектор (переменные), но и векторные операции (функции).

Скалярное произведение векторов

Существует два типа перемножения векторов: векторное и скалярное.

Отличительная особенность скалярного произведения - в результате всегда будет скалярное значение, т.е. число.

Тут стоит обратить внимание вот на какой момент. Если результат данной операции равен нулю, значит, два вектора перпендикулярны - угол между ними 90 градусов. Если результат больше нуля - угол меньше 90 градусов. Если результат меньше нуля, угол больше 90 градусов.

Данную операцию представляет следующая формула:

a · b = a_x*b_x + a_y*b_y + a_z*b_z

Скалярное произведение - это сумма произведений соответствующих компонент двух векторов. Т.е. Берём x'ы двух векторов, перемножаем их, затем складываем с произведением y'ов и так далее.

Векторное произведение векторов

Результатом векторного произведения двух векторов будет вектор перпендикулярный этим векторам.

a x b = <a_y*b_z - a_z*b_y, a_z*b_x - a_x*b_z, a_x*b_y - a_y*b_x>

Мы пока не будем обсуждать подробно эту формулу. К тому же она довольно трудна для запоминания. Мы ещё вернёмся к этому моменту после знакомства с определителями.

Ну и для общего развития полезно знать, что длина полученного вектора, равна площади параллелограмма построенного на векторах a и b.

Нормализация вектора

Нормализованный вектор - это вектор, длина которого равна единице.

Формула для нахождения нормализованного вектора следующая - все компоненты вектора необходимо разделить на его длину:

v_n = v/|v| = <v_x/|v|, v_y/|v|, v_z/|v|>

Послесловие

Как Вы, наверное, убедились, векторы не сложны для понимания. Мы рассмотрели ряд операций над векторами.

В следующих статьях раздела "математика" мы будем обсуждать матрицы, определители, системы линейных уравнений. Это всё теория.

После этого, мы рассмотрим преобразования матриц. Именно тогда Вы поймёте насколько важна математика в создании компьютерных игр. Данная тема как раз и станет практикой по всем предыдущим темам.