Преобразования координатных пространств

Дата создания: 2009-09-10 02:22:29
Последний раз редактировалось: 2012-02-08 09:31:20

Предварительные уроки:
1. Векторы. Перейти.
2. Матрицы. Перейти.
3. Координатные пространства. Перейти.

Дальнейшие уроки
1. Виртуальная камера и перспективная проекция. Перейти.

---

Сначала определимся, что такое преобразования? Допустим у нас есть модель (для простоты, пусть это будет треугольник). И три координатных пространства: объектное (в котором и описан этот треугольник), мировое и пространство камеры. Так вот, преобразование - это выражение координат объекта, находящегося в одной координатной системе (объектной), с помощью координат другой координатной системы (сначала мировой, а потом камерной).

Как я уже писал раньше, использование разных координатных пространств упрощает создание виртуального мира. В объектном пространстве создаются объекты, причём, у каждого объекта есть своё координатное пространство. Мировое пространство связывает все объекты виртуального мира и позволяет сделать очень трудные вещи - очень простыми (например, перемещение объектов). После того как сцена создана и все объекты передвинуты, происходит преобразования мировых координат в координатное пространство камеры. Мы будем использовать только одну камеру, но в реальных ситуациях можно создать несколько. Несколько камер, например, использовалось в гениальной игре Earth 2150: Escape from the blue planet.

Так о чём это я: преобразования необходимы для использования нескольких координатных пространств.

Для начала вспомним кое-что о векторах. В этом нам поможет следующий рисунок:

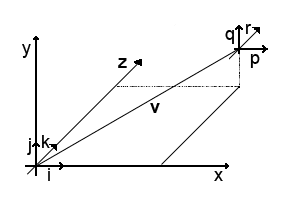
Что же мы здесь видим: мировое пространство координат образованное осями x, y, z. Единичные векторы i, j, k называются ортами или базисными векторами мирового координатного пространства. С помощью суммы этих векторов можно получить любой вектор в мировом координатном пространстве.

v - вектор, который соединяет начало мировых координат и начало объектных координат. Длина вектора v равна расстоянию между началом мировых координат и началом объектных. Рассмотрим векторную форму v=(5,2,5):

v = x*i + y*j + z*k = 5*i + 2*j + 5*k

Как я уже писал выше, с помощью базисных векторов можно представить любую точку (вектор) данного пространства, что и демонстрирует данное уравнение.

Векторы p,q,r - базисные векторы объектного пространства. Заметьте, что i,j,k не обязательно будут равны p,q,r.

На данном рисунке я опустил ряд деталей: в объектном координатном пространстве заданы три точки, которые образуют треугольник. Кроме того, я не обозначил камеру, которая направлена в сторону треугольника.

Линейные преобразования координат с помощью матриц

Для начала давайте рассмотрим единичные векторы i,j,k, которые по направлению совпадают с координатными осями мирового пространства и называются ортами или базисными векторами мирового пространства.

Запишем эти векторы в координатной форме в виде матриц:

i = [ ix iy iz ] = [ 1 0 0 ]
j = [ jx jy jz ] = [ 0 1 0 ]
k = [ kx ky kz ] = [ 0 0 0 ]

Здесь векторы представлены матрицами размером 1x3 (матрицами-строками).

Эти базисные векторы мы можем записать с помощью одной матрицы:

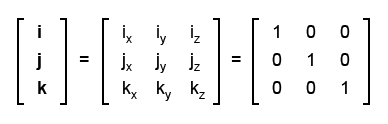
И даже, что намного важнее, можем записать эти векторы вот так:

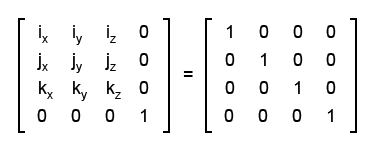
Как видим, получилась единичная матрица размером 3x3 или 4x4.

Казалось бы, что тут такого? Подумаешь, есть возможность записать какие-то дурацкие базисные векторы пространства в одной матрице. Но нет, не "подумаешь"!!! Именно здесь сокрыта одна из самых страшных тайн трёхмерного программирования.

Как я уже писал выше, любая точка, которая присутствует в виртуальном мире, может быть записана в векторной форме:

v = x*i + y*j + z*k

Где v - точка в пространстве, x,y,z - координаты точки v, а i,j,k - базисные векторы пространства. Заметьте, здесь мы говорим о точке, но рассматриваем вектор. Надеюсь вы помните, что вектор и точка - это по сути одно и то же.

Формула выше называется векторной формой вектора. Есть ещё одно название - линейная комбинация векторов. Это так, к слову.

Теперь ещё раз посмотрим на вектор v. Запишем его в матрице-строке: v = [ 5 2 5 ]

Заметьте, что длина вектора v - это расстояние от начала мирового координатного пространства к началу объектного координатного пространства.

Давайте попробуем умножить этот вектор на матрицу в которой записаны базисные векторы мирового пространства (надеюсь вы помните формулу перемножения матриц):

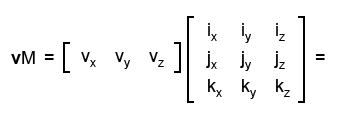
В итоге мы получим следующее уравнение:

vM = [ (xix + yjx + zkx)  (xiy + yjy + zky) (xiz +yjz + zkz) ]

Мы получили вектор. Т.е. результатом перемножения вектора на матрицу, является вектор. В данном случае, вектор не изменился. Но если элементами матрицы будут не единицы (на главной диагонали) и нули (все остальные элементы), а какие-нибудь другие числа, то вектор изменится. Поэтому можно говорить, что матрица M выполняет преобразование координатных пространств. Рассмотрим общую формулу:

aM = b

a, b - векторы, M - матрица преобразования координатных пространств. Формулу можно прочитать так: "матрица M преобразовывает точку a в точку b".

Для наглядности давайте рассмотрим пример. Нам нужно преобразовать координаты из объектного пространства (p,q) в мировое (i,j):

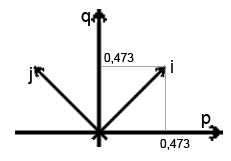
i,j - базисные векторы мирового пространства, p,q - базисные векторы объектного пространства. На картинке можно увидеть, что объектное координатное пространство повёрнута на -45 градусов вокруг оси z (на рисунке её не видно). Кроме того, векторы q,p в 1,5 раза больше векторов i,j, а это значит, что объекты определённые в объектном пространстве, в мировом пространстве будут выглядеть в полтора раза меньше.

Чтобы наглядно представить, как модель объектного пространства будет выглядеть после преобразования можно дорисовать рамку для векторов i,j:

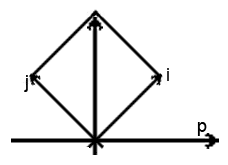
Можно такую же рамку нарисовать и для p,q, но я не стал загромождать рисунок.

Теперь, допустим, в объектном пространстве у нас нарисован треугольник (рис. а). В мировом пространстве этот треугольник будет повёрнут на 45 градусов и уменьшен на одну треть (рис. б):

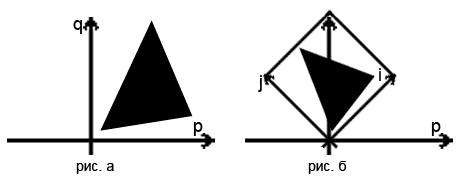
Теперь соберём все элементы мозайки: как мы знаем, преобразование можно сделать с помощью матрицы. Строками матриц являются базисные векторы. Координаты базисных векторов мирового координатного пространства в объектном пространстве следующие:

i = [  0.473  0.473 ]
j = [ -0.473  0.473 ]

Как мы узнали координаты? Во-первых, мы знаем, что координатные пространства повёрнуты друг относительно друга на 45 градусов. Во-вторых, базисные векторы объектного пространства в 1,5 раза длинее базисных векторов мирового пространства. Зная это, мы легко вычислили координаты векторов i,j.

В итоге у нас получается вот такая матрица преобразования (в данном случае - поворота или вращения):

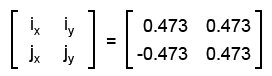
Или в трёхмерном пространстве:

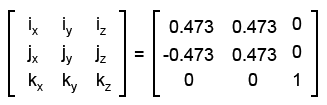
Все значения - приблизительные.

Это матрица преобразования координат из объектного пространства в инерционное (напоминаю, что базисные векторы инерционного пространства совпадают с базисными векторами мирового пространства). Чтобы преобразовать треугольник из объектного пространства в инерционное, нужно умножить все точки (векторы) треугольника на матрицу преобразования.

В последнем примере мы повстречались с двумя преобразованиями: поворот и масштабирование. Оба этих преобразовиния являются линейными.

Теперь, когда мы рассмотрели примеры линейных преобразования, можно познакомиться и с определением:

Линейные преобразования - это преобразования координат, при которых не происходит искажения пространств. Т.е. все параллельные прямые остаются параллельными (есть правда одно исключение). Или совсем по простому: при линейных преобразованиях треугольник никогда не превратится в круг или в квадрат, а всегда будет оставаться треугольником.

Теперь, когда мы приблизительно понимаем, что такое линейные преобразования, рассмотрим конкретные формулы:

Масштабирование (Scale)

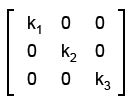
k₁,k₂,k₃ - коффициенты масштабирования. Если k < 1, значит происходит уменьшение объектов, если k > 1, происходит увеличение объектов.

Поворот или вращение (Rotation)

Вращение против часовой стрелки будем считать положительным.

Поворот вокруг оси x:

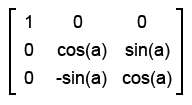
Поворот вокруг оси y:

Поворот вокруг оси z:

Кстати, именно эту матрицу (поворота вокруг оси z) мы использовали выше.

Вращение может быть не только вокруг осей образующих координатное пространство, но и вокруг произвольных прямых. Формула поворота вокруг произвольной прямой довольно сложна, мы пока не готовы её рассмотреть.

Самое важное, что вы должны запомнить из вышеизложенного, следующее: строки матрицы преобразования содержат базисные векторы нового координатного пространства, выраженные через координаты старого координатного пространства..

Если понять эту простую вещь (что в матрице записаны базисные векторы нового пространства), то глядя на матрицу преобразования, можно легко увидеть новое координатное пространство.

И последнее:
С помощью линейных преобразований нельзя перемещать объекты. Т.е. объекты могут быть увеличены/уменьшены, их можно вращать, но они останутся неподвижными.

Аффинные преобразования

Аффинные преобразования - это линейные преобразования с переносом. С помощью аффинных преобразований можно передвигать объекты.

Формула очень простая:

a = bM + v;

Где b - исходная точка, M - матрица линейного преобразования, a - преобразоавнная точка и v - вектор, соединяющий два пространства. Или другими словами, это вектор, длина которого равна расстоянию между двумя координатными пространствами.

На картинке в начале урока необходимо именно аффинное преобразование: сначала линейное преобразование из объектного пространства в инерционное, а затем перенос всех точек объектного пространства в мировое с помощью вектора v.

Однородная система координат

Для упрощения вычислений в программировании трёхмерной графики используются четырёхмерные векторы, матрицы размером 4x4 и так называемые однородные координаты. Четвёртое измерение не играет никакой роли, оно вводится только лишь для упрощения вычислений.

В четырёхмерном векторе, как вы возможно догадались, используются четыре компоненты: x, y, z и w. Четвёртая компонента вектора назывется однородной координатой.

Геометрически представить однородную координату очень сложно. Поэтому мы рассмотрим трёхмерное однородное пространство с координатами (x,y,w). Представим что двухмерная плоскость определа в точке w=1. Соответственно двухмерная точка представлена в однородном пространстве следующими координатами (x,y,1). Все точки пространства, которые не находятся в плоскости (они находятся в плоскостях, где w != 1) можно вычислить спроецировав на двухмерную плоскость. Для этого нужно разделить все компоненты этой точки на однородную. Т.е. если w!=1, в "физической" (там где мы работаем и там где w=1) плоскости координаты точки будут следующими: (x/w,y/w,w/w) или (x/w,y/w,1). Посмотрите на рисунок:

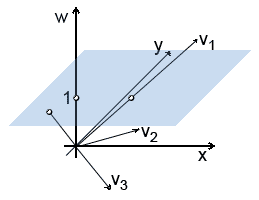
Координаты векторов следующие:

v1 = [ 3  3 3 ]
v2 = [ 3  1 0 ]
v3 = [ 3 -2 -2 ]

Эти векторы спроецируются в "физическую" плоскость (w=1) следующим образом:

v1 = [  1    1  1 ]
v3 = [ -1.5  1  1 ]

На рисунке видно три вектора. Обратите внимание, что когда точка лежит в плоскости w=0, то эту точку нельзя спроецировать в физическую плоскость (вектор v₂).

Для каждой точки физической плоскости существует бесконечное количество точек в однородном пространстве.

В четырёхмерном пространтстве всё точно так же. Мы работаем в физическом пространстве где w = 1: (x,y,z,1). Если в результате вычислений w != 1, значит нужно все координаты точки разделить на однородную: (x/w,y/w,z/w,w/w) или (x/w,y/w,z/w,1). Существует ещё особый случай, когда w = 0. Мы его рассмотрим попозже.

Теперь перейдём к практике: для чего же чёрт возьми нужна однородная координата?

Как мы уже выяснили, матрица размером 3x3 представляет линейное преобразование, т.е. в ней не содержится переноса (перемещения). Для переноса используется отдельний вектор (а это уже аффинное преобразование):

v = aM + b

Т.е. мы умножаем все точки (векторы) объекта на матрицу преобразования M, чтобы перейти в инерционную систему координат (базисные векторы которой совпадают с базисными векторами мировой системы координат), а затем добираемся до мирового пространства с помощью вектора b. Напоминаю, что вектор b соединяет начало объектного пространства и начало мирового пространства.

Так вот, используюя четыре измерения можно в одну матрицу запихать как линейные преобразования (вращение, масштабирование), так и перенос.

Представим, что четвёртая компонента всегда равна единице (хотя, мы уже выяснили что это не так). Теперь линейное преобразование можно представить с помощью матрицы размером 4x4:

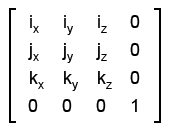
Посмотрим на формулу умножения векторов на матрицу преобразования в четырёхмерном пространстве:

vx = (xix + yjx + zkx + w*0)
vy = (xiy + yjy + zky + w*0)
vz = (xiz + yjz + zkz + w*0)
vw = (x*0 + y*0 + z*0 + w*1)

Как видим, компоненты преобразованного вектора с помощью матрицы размером 4x4, равны компонентам преобразованного вектора с помощью матрицы размером 3x3. Четвёртая же компонента, как мы условились, всегда будет равна единице, поэтому её можно просто отбросить. Следовательно, можно сказать, что преобразования осуществляемые матрицами размером 3x3 и 3x4 - эквиваленты.

Теперь посмотрим на матрицу переноса:

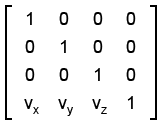
Умножьте любой вектор из объектного пространства (смотрите рисунок в начале урока) на данную матрицу и вы сможете выразить этот вектор в мировом координатном пространстве (это если базисные векторы объектного и мирового пространств равны).

Обратите внимание, что это тоже линейное преобразование, только в четырёхмерном пространстве.

С помощью произведения матриц мы можем объединить матрицу вращения и матрицу переноса:

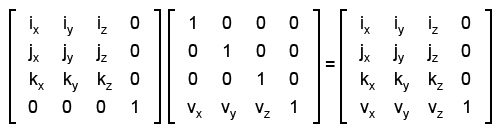
Вот эта последняя матрица именно то, что нам было нужно с самого начала. Вы должны хорошо понимать что именно значат все её элементы (за исключением 4-ого столбца).