Преобразования: Последняя битва
Дата создания: 2009-10-20 03:43:37
Последний раз редактировалось: 2012-02-08 09:36:52
- Предварительные уроки:
- Тригонометрия. Перейти.
- Векторы. Перейти.
- Матрицы. Перейти.
- Координатные пространства. Перейти.
- Преобразования координатных пространств. Перейти.
- Перспективная проекция. Перейти.
Что-то мы давненько не вспоминали о преобразованиях! Наверное, мой дорогой читатель, ты уже соскучился по ним? Как показывает практика, преобразования - самая любимая тема у изучающих трёхмерное программирование.
На данный момент вы уже должны хорошо разбираться в преобразованиях. Если же нет, то смотрите предварительные уроки.
Когда мы только начинали изучать преобразования, я писал, что с помощью матриц можно манипулировать предметами в пространстве: перемещать, вращать, увеличивать. Если вы изучили все предыдущие уроки и попытались применить полученные знания на практике, то скорее-всего вам пришлось столкнуться с определёнными трудностями: как передвигать предметы в произвольном направлении, как же всё-таки составить матрицу для преобразования в пространство камеры, как вращать предметы в произвольном направлении? Рассмотрением этих вопросов мы и займёмся сегодня.
Перемещение в пространстве
Небольшое замечание: мировое пространство координат мы будем обозначать осями x,y,z. Базисные векторы, образующие локальное (объектное, камеры) пространство мы будем обозначать как i=(1,0,0), j=(0,1,0), k=(0,0,1) (названия векторов читаются как: и, жи, ка). Вектор i - параллелен оси x, вектор j - оси y, вектор k - оси z.
Напоминаю, что с помощью линейной комбинации (суммы) базисных векторов можно выразить любой вектор пространства. Также не забываем о том, что длина базисных векторов равна единице.
Теперь смотрим на картинку:
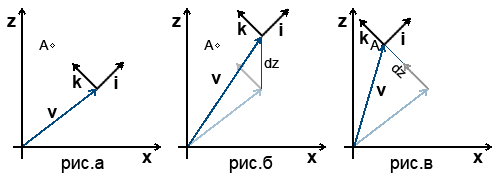
Для простоты мы отбросили одно измерение - вертикальное. Соответственно на картинках изображён вид сверху.
Допустим мы находимся в какой-то точке мирового пространства. В данном случае под местоимением "мы" можно подразумевать что угодно: объект в игровом мире, персонаж, камеру. В данном случае (рис.а) мы смотрим в сторону точки A. Откуда мы знаем, что "взгляд" направлен в сторону точки A? Ну, когда мы обсуждали камеры, то договорились, что вектор k указывает направление взгляда.
От центра мира (мирового пространства координат) нас отделяет вектор v. И вдруг! Нам страшно захотелось подойти к точке A. Первая мысль: снять со стрелочки "вперёд" значение (dz) и прибавить к третьей компоненте вектора v. Результат этого недоразумения можно увидеть на рис.б. Казалось бы, всё пропало - прощайте мечты о собственном квейке. Отставить панику! Нужно просто тщательно обдумать сложившуюся ситуацию.
Представим, что мы уже находимся в точке A - посмотрим на рис.в. Как видно из рисунка, после перемещения векторы k и i не изменились. Соответственно мы их трогать и не будем.
Смотрим на оставшуюся часть картинки: вектор v после перемещения - это сумма двух векторов: вектора v до перемещения и неизвестного нам вектора, совпадающего по направлению с вектором k... А ведь мы теперь можем легко найти неизвестный вектор!
Если вы внимательно изучали урок про векторы, то вы помните, что умножение скаляра на вектор увеличивает (если скаляр больше единицы) вектор. Поэтому неизвестный вектор равен k*dz. Соответственно вектор v после перемещения можно найти по формуле:
v = v + k*dz
Ну разве не просто?
Вращение вокруг осей
Мы уже знаем формулы вращения вокруг осей. В этом разделе я просто более наглядно их поясню. Рассмотрим вращение двух векторов вокруг центра координат в двухмерном пространстве.
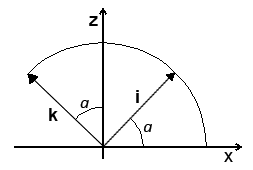
Так как мы знаем угол поворота (угол альфа), то координаты базисных векторов пространства можно легко вычислить с помощью тригонометрических функций:
i.x = cos(a); i.z = sin(a); k.x = -sin(a); k.y = cos(a);
Теперь посмотрим на матрицы вращения вокруг осей в трёхмерном пространстве и на соответствующие иллюстрации.
Вращение вокруг оси x:
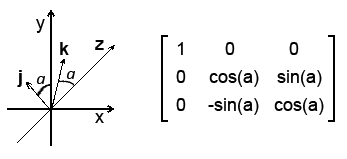
Вращение вокруг оси y:
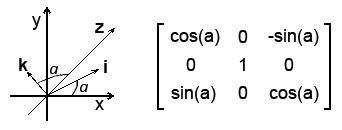
Вращение вокруг оси z:

На рисунках показано какие именно векторы меняют свои координаты.
Небольшое замечание: неверно говорить о вращении вокруг осей. Вращение происходит вокруг векторов. Мы не умеем представлять прямые (оси) в памяти компьютера. А вот векторы - запросто.
И ещё одно: как определяется положительный и отрицательный угол вращения? Это легко: нужно "встать" в центр координат и смотреть в сторону положительного направления оси (прямой). Вращение против часовой стрелки - положительное, по часовой - отрицательное. Соответственно на рисунках выше углы вращения вокруг x и y - отрицательные, а угол вращения вокруг оси z - положительный.
Вращение вокруг произвольной прямой
Представьте такую ситуацию: вы поворачиваете камеру с помощью матрицы вокруг оси x (наклоняете камеру) на двадцать градусов. Теперь вам нужно повернуть камеру на двадцать градусов вокруг оси y. Да без проблем, скажете вы... Стоп! А вокруг чего теперь нужно поворачивать объект? Вокруг оси y, которая была до предыдущего поворота или после? Ведь это две совершенно разные оси. Если вы просто создадите две матрицы вращения (вокруг оси x и вокруг оси y) и перемножите их, то второй поворот будет осущетсвлён вокруг первоначальной оси y. А что если нам необходим второй вариант? В данном случае нам нужно будет научиться вращать объекты вокруг произвольной прямой. Но сначала небольшой тест:
Сколько векторов на следующей картинке?
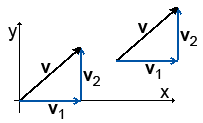
Правильнй отвект - три вектора. Помните: векторы - это длина и направление. Если в пространстве два вектора имеют одинаковую длину и направление, но находятся в разных местах, то можно считать, что это один и тот же вектор. Кроме того, на рисунке я изобразил сумму векторов. Вектор v = v1 + v2.
В уроке по векторам мы кратко рассмотрели скалярное и векторное произведение векторов. К сожалению, мы не изучили эту тему более подробно. В формуле ниже будет использоваться и скалярное, и векторное произведение. Поэтому буквально пару слов: значение скалярного произведение - это проекция первого вектора на второй. При векторном произведении двух векторов: a x b = c, вектор c перпендикулярен векторам a и b.
Смотрим на следующий рисунок: в пространстве определён вектор v. И данный вектор нужно повернуть вокруг прямой l (эль):
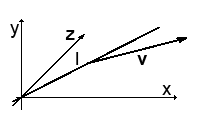
Мы не умеем представлять прямые в программах. Поэтому прямую мы представим в виде единичного вектора n, который совпадает по направлению с прямой l (эль). посмотрим на более подробный рисунок:
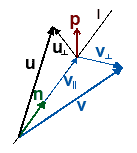
Что у нас есть:
1. Прямая l представленная вектором единичной длины n. Как уже писалось выше, вращение вектора v будет осуществляться вокруг вектора, а не прямой.
2. Вектор v, который нужно повернуть вокруг вектора n. В результате вращения у нас должен получиться вектор u (читается как у).
3. Угол, на который нужно осуществить вращение вектора v.
Зная эти три величины, мы должны выразить вектор u.
Вектор v можно представить как сумму из двух векторов: v = v⊥ + v||. При этом вектор v|| - параллелен вектору n (можно даже сказать: v|| - проекция v на n), а вектор v⊥ перпендикулярен n. Как несложно догадаться, поворачивать нужно только перпендикулярную вектору n часть вектора v. То есть - v⊥.
На рисунке присутствует ещё один вектор - p. Этот вектор перпендикулярен плоскости образованной векторами v|| и v⊥, |v⊥| = |p| (длины этих векторов равны) и p = n x v.
u⊥ = v⊥cosa + psina
Если непонятно почему u⊥ вычисляется именно так, вспомните что такое синус и косинус и что представляет собой умножение скалярного значения на вектор.
Теперь нужно из последнего уравнения убрать v⊥ и p. Делается это с помощью простых подстановок:
v|| = n(v · n) v⊥ = v - v|| = v - n(v · n) p = n x v u|| = v|| u⊥ = v⊥cosa + psina = (v - n(v · n))cosa + (n x v)sina u = u⊥ + v|| = (v - n(v · n))cosa + (n x v)sina + n(v · n)
Вот такая вот загогулина! Это формула поворота вектора v на угол a (альфа) вокруг вектора n. Теперь с помощью этой формулы мы можем вычислить базисные векторы:
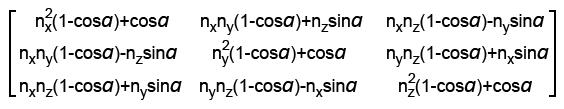
Упражнения
1. Обязательное: подставьте базисные векторы в формулу вращения вектора вокруг произвольной прямой. Посчитайте (с помощью карандаша и листка бумаги). После всех упрощений у вас должны получиться базисные векторы как на последней картинке. Упражнение займёт у вас минут десять.
Вот и всё.